
| AB |
| AC |
| 3 |
| 1 |
| 2 |
| 1 |
| x |
| 4 |
| y |
| AB |
| AC |
| 3 |
| AC |
| AB |
| 3 |
| AC |
| AB |
| 1 |
| 2 |
| AC |
| AB |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| x |
| 4 |
| y |
| 1 |
| x |
| 4 |
| y |
| 2y |
| x |
| 8x |
| y |
|
| 2y |
| x |
| 8x |
| y |
| 1 |
| x |
| 4 |
| y |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练10练习卷(解析版) 题型:填空题
设M是△ABC内一点,且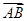 ·
·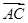 =2
=2 ,∠BAC=30°,定义f(M)=(m,n,p),其中m、n、p分别是△MBC、△MCA、△MAB的面积,若f(M)=(
,∠BAC=30°,定义f(M)=(m,n,p),其中m、n、p分别是△MBC、△MCA、△MAB的面积,若f(M)=(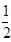 ,x,y),则
,x,y),则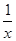 +
+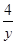 的最小值是 .
的最小值是 .
查看答案和解析>>
科目:高中数学 来源:2010-2011学年辽宁省沈阳市四校协作体高三12月月考数学文卷 题型:选择题
设M是△ABC内一点,且 =2
=2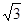 ,∠BAC=30°定义f(M)=(m,n,p),其中m,n,p分别是△MBC,△MCA, △MAB的面积.若f(M)=(
,∠BAC=30°定义f(M)=(m,n,p),其中m,n,p分别是△MBC,△MCA, △MAB的面积.若f(M)=( ,x,y),则
,x,y),则 的最小值是
的最小值是
A.20 B.18 C.16 D.14
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省淮安市盱眙县新海高级中学高三(上)10月学情调研数学试卷(理科)(解析版) 题型:填空题
 的最大值和最小值分别为M和N,则M+N= .
的最大值和最小值分别为M和N,则M+N= .查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省某重点中学高一(上)10月月考数学试卷(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com