
【题目】已知函数 ![]() 存在两个极值点.
存在两个极值点.
(Ⅰ)求实数a的取值范围;
(Ⅱ)设x1和x2分别是f(x)的两个极值点且x1<x2 , 证明: ![]() .
.
【答案】解:(Ⅰ)由题设函数f(x)的定义域为(0,+∞),f'(x)=lnx﹣ax,
故函数f(x)有两个极值点等价于其导函数f'(x)在(0,+∞)有两个零点.
当a=0时f'(x)=lnx,显然只有1个零点x0=1.
当a≠0时,令h(x)=lnx﹣ax,那么 ![]() .
.
若a<0,则当x>0时h'(x)>0,即h(x)单调递增,所以h(x)无两个零点.
若a>0,则当 ![]() 时h'(x)>0,h(x)单调递增;当
时h'(x)>0,h(x)单调递增;当 ![]() 时h'(x)<0,h(x)单调递减,
时h'(x)<0,h(x)单调递减,
所以 ![]() .
.
又h(1)=﹣a<0,当x→0时→﹣∞,故若有两个零点,则 ![]() ,得
,得 ![]() .
.
综上得,实数a的取值范围是 ![]() .
.
(Ⅱ)证明:要证 ![]() ,两边同时取自然对数得
,两边同时取自然对数得 ![]() .
.
由f'(x)=0得 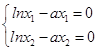 ,得
,得 ![]() .
.
所以原命题等价于证明 ![]() .
.
因为x1<x2,故只需证 ![]() ,即
,即 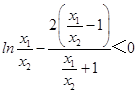 .
.
令 ![]() ,则0<t<1,设
,则0<t<1,设 ![]() ,只需证g(t)<0.
,只需证g(t)<0.
而 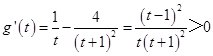 ,故g(t)在(0,1)单调递增,所以g(t)<g(1)=0.
,故g(t)在(0,1)单调递增,所以g(t)<g(1)=0.
综上得 ![]() .
.
【解析】(Ⅰ)函数f(x)有两个极值点等价于其导函数f'(x)在(0,+∞)有两个零点,分类讨论求实数a的取值范围;(Ⅱ)要证 ![]() ,两边同时取自然对数得
,两边同时取自然对数得 ![]() ,由f'(x)=0得
,由f'(x)=0得 ![]() ,得
,得 ![]() .所以原命题等价于证明
.所以原命题等价于证明 ![]() .
.
【考点精析】掌握利用导数研究函数的单调性和函数的极值与导数是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


科目:高中数学 来源: 题型:
【题目】设等差数列{an}满足(1﹣a1008)5+2016(1﹣a1008)=1,(1﹣a1009)5+2016(1﹣a1009)=﹣1,数列{an}的前n项和记为Sn , 则( )
A.S2016=2016,a1008>a1009
B.S2016=﹣2016,a1008>a1009
C.S2016=2016,a1008<a1009
D.S2016=﹣2016,a1008<a1009
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了了解一年内的用水情况,抽取了10天的用水量如下表所示:
天数 | 1 | 1 | 1 | 2 | 2 | 1 | 2 |
用水量/吨 | 22 | 38 | 40 | 41 | 44 | 50 | 95 |
(Ⅰ)在这10天中,该公司用水量的平均数是多少?每天用水量的中位数是多少?
(Ⅱ)你认为应该用平均数和中位数中的哪一个数来描述该公司每天的用水量?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在各项为正的数列{an}中,数列的前n项和Sn满足Sn= ![]() (an+
(an+ ![]() ),
),
(1)求a1 , a2 , a3;
(2)由(1)猜想数列{an}的通项公式,并用数学归纳法证明你的猜想.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下命题正确的个数为( ) ①存在无数个α,β∈R,使得等式sin(α﹣β)=sinαcosβ+cosαsinβ成立;
②在△ABC中,“A> ![]() ”是“sinA>
”是“sinA> ![]() ”的充要条件;
”的充要条件;
③命题“在△ABC中,若sinA=sinB,则A=B”的逆否命题是真命题;
④命题“若α= ![]() ,则sinα=
,则sinα= ![]() ”的否命题是“若α≠
”的否命题是“若α≠ ![]() ,则sinα≠
,则sinα≠ ![]() ”.
”.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+ ![]() (a,b∈R)的图象过点P(1,f(1)),且在点P处的切线方程为y=3x﹣8.
(a,b∈R)的图象过点P(1,f(1)),且在点P处的切线方程为y=3x﹣8.
(Ⅰ)求a,b的值;
(Ⅱ)求函数f(x)的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大西洋鲑鱼每年都要逆流而上,游回产地产卵,研究鲑鱼的科学家发现鲑鱼的游速![]() (单位:
(单位: ![]() )与其耗氧量单位数
)与其耗氧量单位数![]() 之间的关系可以表示为函数
之间的关系可以表示为函数![]() ,其中
,其中![]() 为常数,已知一条鲑鱼在静止时的耗氧量为100个单位;而当它的游速为
为常数,已知一条鲑鱼在静止时的耗氧量为100个单位;而当它的游速为![]() 时,其耗氧量为2700个单位.
时,其耗氧量为2700个单位.
(1)求出游速![]() 与其耗氧量单位数
与其耗氧量单位数![]() 之间的函数解析式;
之间的函数解析式;
(2)求当一条鲑鱼的游速不高于![]() 时,其耗氧量至多需要多少个单位?
时,其耗氧量至多需要多少个单位?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com