
 ,则该球的表面积为________cm3.
,则该球的表面积为________cm3. ,根据球的截面圆性质,算出球半径R=
,根据球的截面圆性质,算出球半径R= =4,代入球的表面积公式即算出该球的表面积.
=4,代入球的表面积公式即算出该球的表面积.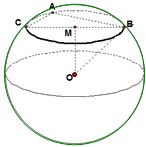
 =4
=4 ,可得半径r=2
,可得半径r=2

 =4
=4

 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
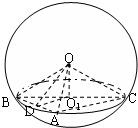 如图,已知A,B,C是表面积为48π的球面上的三点,AB=2,BC=4,∠ABC=60°,O为球心,则二面角O-AB-C的大小为:( )
如图,已知A,B,C是表面积为48π的球面上的三点,AB=2,BC=4,∠ABC=60°,O为球心,则二面角O-AB-C的大小为:( )A、
| ||||
B、
| ||||
C、arccos
| ||||
D、arccos
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:高中数学 来源:高考零距离 二轮冲刺优化讲练 数学 题型:013
已知A、B、C是球面上的三点,且AB=6,BC=8,AC=10,球心O到平面A B C的距离为![]() ,则球的表面积为
,则球的表面积为
A.36π
B.72π
C.144π
D.288π
查看答案和解析>>
科目:高中数学 来源:2013年上海市黄浦区高考数学二模试卷(理科)(解析版) 题型:填空题
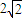 ,则该球的表面积为 cm3.
,则该球的表面积为 cm3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com