由曲线y2=2x 和直线y=x-4所围成的图形的面积为 .
【答案】
分析:先求出曲线y
2=2x 和直线y=x-4的交点坐标,从而得到积分的上下限,然后利用定积分表示出图形面积,最后根据定积分的定义求出即可.
解答:解:
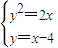
解得曲线y
2=2x 和直线y=x-4的交点坐标为:(2,-2),(8,4)
选择y为积分变量
∴由曲线y
2=2x 和直线y=x-4所围成的图形的面积S=

=(

y
2+4y-

y
3)|
-24=18
故答案为:18
点评:本题主要考查了定积分在求面积中的应用,以及会利用定积分求图形面积的能力.应用定积分求平面图形面积时,积分变量的选取是至关重要的,属于基础题.
