练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在梯形ABCD中，AB∥CD，AD＝DC＝CB＝1，∠BCD＝120°，四边形BFED为矩形，平面BFED⊥平面ABCD，BF＝1．

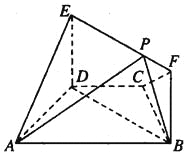
    （1）求证：AD⊥平面BFED；

    （2）已知点P在线段EF上，＝2．求三棱锥E－APD的体积．

    【答案】（1）证明详见解析；（2）.

    【解析】

    试题分析: 本题主要考查线面垂直的判定与性质、空间几何体体积等基础知识，考查学生的分析问题解决问题的能力、空间想象能力、逻辑推理能力、计算能力. 第一问，在中，利用余弦定理计算出的值，可以看出，符合勾股定理，得到，再由面面垂直的性质定理得线面垂直，从而得，最后由线面垂直的判定定理得到结论；第二问，由线面垂直的性质得即是锥体的高，用等体积转化法将转化为，用体积公式计算.

    试题解析：（1）在梯形中，

    ∵∥，

    ∴∴

    ∴∴∵平面平面

    平面平面 ，

    ∴

    ∴又∴

    （2）由（1）知⊥平面

    ∵//, ∴且

    ∴

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某食品店为了了解气温对销售量的影响，随机记录了该店1月份中5天的日销售量（单位：千克）与该地当日最低气温（单位： ）的数据，如下表：

    2

    5

    8

    9

    11

    12

    10

    8

    8

    7

    （1）求出与的回归方程；

    （2）判断与之间是正相关还是负相关；若该地1月份某天的最低气温为6，请用所求回归方程预测该店当日的营业额.

    附: 回归方程中， ,

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（是自然对数的底数，）.

    （1）求函数的单调递增区间；

    （2）若为整数，，且当时，恒成立，其中为的导函数，求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】执行如图所示的程序框图，则输出的S值为（ ）
    A.1009
    B.﹣1009
    C.﹣1007
    D.1008

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，角A，B，C的对边分别为a，b，c，btanB+btanA=﹣2ctanB，且a=8，△ABC的面积为 ，则b+c的值为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线l的参数方程为 （t为参数），以坐标原点为极点，x轴的非负半轴为极轴，建立极坐标系，圆C的极坐标方程为ρ=4cosθ，直线l与圆C交于A，B两点．
    （1）求圆C的直角坐标方程及弦AB的长；
    （2）动点P在圆C上（不与A，B重合），试求△ABP的面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C： =1（a＞b＞0）的左焦点为F，直线y=kx（k＞0）与椭圆C交于A，B两点，若 ，则C的离心率取值范围为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从边长为2a的正方形铁片的四个角各截去一个边长为x的正方形，然后折成一个无盖的长方体盒子，要求长方体的高度x与底面正方形边长的比不超过正数t.

    (1)把铁盒的容积V表示为关于x的函数，并指出其定义域．

    (2)当x为何值时，容积V有最大值？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数f（x）=x2﹣ex﹣ax在R上存在单调递增区间，则实数a的取值范围是 ．

    查看答案和解析>>

    同步练习册答案