
【题目】已知函数![]() .
.
![]() 讨论
讨论![]() 函数的单调性;
函数的单调性;
![]() 设
设![]() 的两个零点是
的两个零点是![]() ,
, ![]() ,求证:
,求证: ![]() .
.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设圆![]() 满足:(1)截
满足:(1)截![]() 轴所得弦长为2;(2)被
轴所得弦长为2;(2)被![]() 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为![]() .在满足条件(1)、(2)的所有圆中,圆心到直线
.在满足条件(1)、(2)的所有圆中,圆心到直线![]() 的距离最小的圆的方程为__________.
的距离最小的圆的方程为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知几何体A﹣BCED的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形. 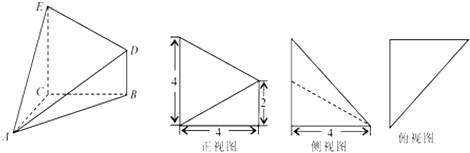
(1)求此几何体的体积V的大小;
(2)求异面直线DE与AB所成角的余弦值;
(3)求二面角A﹣ED﹣B的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿海准备购买“海马”牌一辆小汽车,其中购车费用12.8万元,每年的保险费、汽油费约为0.95万元,年维修、保养费第一年是0.1万元,以后逐年递增0.1万元.请你帮阿海计算一下这种汽车使用多少年,它的年平均费用最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设不等式组 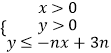 所表示的平面区域为Dn , 记Dn内的格点(格点即横坐标和纵坐标皆为整数的点)的个数为f(n)(n∈N*).
所表示的平面区域为Dn , 记Dn内的格点(格点即横坐标和纵坐标皆为整数的点)的个数为f(n)(n∈N*).
(1)求f(1)、f(2)的值及f(n)的表达式;
(2)设bn=2nf(n),Sn为{bn}的前n项和,求Sn;
(3)记 ![]() ,若对于一切正整数n,总有Tn≤m成立,求实数m的取值范围.
,若对于一切正整数n,总有Tn≤m成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了了解高二年级学生对教师教学的意见,打算从高二年级883名学生中抽取80名进行座谈,若采用下面的方法选取:先用简单随机抽样从883人中剔除3人,剩下880人再按系统抽样的方法进行,则每人入选的概率是( )
A.![]()
B.![]()
C.![]()
D.无法确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1 . 求证: 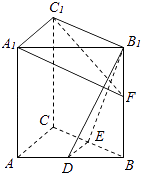
(1)直线DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(k)是满足不等式log2x+log2(52k﹣1﹣x)≥2k(k∈N*)的自然数x的个数.
(1)求f(k)的函数解析式;
(2)Sn=f(1)+2f(2)+…+nf(n),求Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com