设一个椭圆的焦距、短轴长、长轴长成等比数列,则此椭圆的离心率e= .
【答案】
分析:设出椭圆的焦距、短轴长、长轴长分别为2c,2b,2a,通过椭圆的2c,2b,2a是等比数列建立关于a,b,c的等式,求出椭圆的离心率即可.
解答:解:设出椭圆的焦距、短轴长、长轴长分别为2c,2b,2a,
∵椭圆的焦距、短轴长、长轴长成等比数列,
∴2c,2b,2a成等比数列,
∴4b
2=2a•2c,∴b
2=a•c
∴b
2=a
2-c
2=a•c,
两边同除以a
2得:e
2+e-1=0,
解得,e=

,
故答案为:
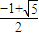
.
点评:本题考查椭圆的基本性质,等比数列性质的应用,考查计算能力,属于基础题.
