
【题目】在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,∠APD=90°,PA=PD=AB=a,ABCD是矩形,E是PD的中点. 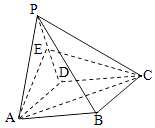
(1)求证:PB⊥AC.
(2)求二面角E﹣AC﹣D的正切值.
【答案】
(1)证明:设AD中点为F连接BF、PF.
∵PA=PD=AB=a,∴ ![]() ,
,
∴ ![]() .
.
∴△ABC∽△FAB,∴AC⊥BF,
又∵PF⊥AD,又∵平面PAD⊥平面ABCD.
平面PAD∩平面ABCD=AD,
∴PF⊥面ABC,∴PF⊥AC,
∴AC⊥平面PBF,AC⊥PB.
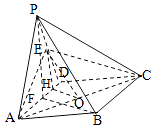
(2)解:(2)过E作EH∥PF,EH交AD于H,
过H作HO⊥AC,交AC于O,连接EO.
由(1)知EH⊥面ACD,HO⊥AC,
∴∠EOH为二面角E﹣AC﹣D的平面角
![]() .
.
![]() .
.
∴ ![]() .
.
∴二面角E﹣AC﹣D的正切值为 ![]() .
.
【解析】(1)设AD中点为F,连接BF、PF,推导出△ABC∽△FAB,从而AC⊥BF,推导出PF⊥AC,由此能证明AC⊥PB.(2)过E作EH∥PF,EH交AD于H,过H作HO⊥AC,交AC于O,连接EO,则∠EOH为二面角E﹣AC﹣D的平面角,由此能求出二面角E﹣AC﹣D的正切值.
【考点精析】解答此题的关键在于理解直线与平面垂直的性质的相关知识,掌握垂直于同一个平面的两条直线平行.


科目:高中数学 来源: 题型:
【题目】在△ABC中,分别根据下列条件解三角形,其中有两解的是( )
A.a=7,b=14,A=30°
B.b=4,c=5,B=30°
C.b=25,c=3,C=150°
D.a= ![]() ,b=
,b= ![]() ,B=60°
,B=60°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}满足a1=1,(n+1)a2n+1+an+1an﹣na ![]() =0,数列{bn}的前n项和为Sn且Sn=1﹣bn .
=0,数列{bn}的前n项和为Sn且Sn=1﹣bn .
(1)求{an}和{bn}的通项;
(2)令cn= ![]() , ①求{cn}的前n项和Tn;
, ①求{cn}的前n项和Tn;
②是否存在正整数m满足m>3,c2 , c3 , cm成等差数列?若存在,请求出m;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新课标要求学生数学模块学分认定由模块成绩决定,模块成绩由模块考试成绩和平时成绩构成,各占50%,若模块成绩大于或等于60分,获得2学分,否则不能获得学分(为0分),设计一算法,通过考试成绩和平时成绩计算学分,并画出程序框图.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建设一仓库,设AB=ykm,并在公路北侧建造边长为xkm的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且∠ABC=60°。 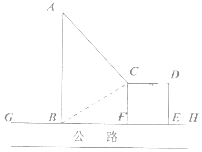
(1)求y关于x的函数解析式,并求出定义域;
(2)如果中转站四堵围墙造价为10万元/km,两条道路造价为30万元/km,问:x取何值时,该公司建设中转站围墙和两条道路总造价M最低.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生身高情况,某校以 ![]() 的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为
的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为 ![]() ,测得男生身高情况的频率分布直方图(如图所示):
,测得男生身高情况的频率分布直方图(如图所示):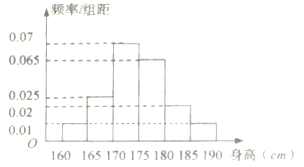
(1)计算所抽取的男生人数,并估计男生身高的中位数(保留两位小数);
(2)从样本中身高在 ![]() 之间的男生中任选2人,求至少有1人身高在
之间的男生中任选2人,求至少有1人身高在 ![]() 之间的概率.
之间的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com