
【题目】已知点![]() 是圆
是圆![]() 上的任意一点,点
上的任意一点,点![]() 为圆
为圆![]() 的圆心,点
的圆心,点![]() 与点
与点![]() 关于平面直角系的坐标原点对称,线段
关于平面直角系的坐标原点对称,线段![]() 的垂直平分线与线段
的垂直平分线与线段![]() 交于点
交于点![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若轨迹![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,直线
,直线![]() 交轨迹
交轨迹![]() 于
于![]() 两点,求
两点,求![]() 面积的取值范围.
面积的取值范围.
【答案】(1)![]() (2)
(2)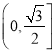
【解析】试题分析:(1)根据圆的的性质及对称的几何性质可得,动点![]() 的轨迹是以
的轨迹是以![]() 为焦点,4为长轴长的椭圆,从而可得结果;(2)把直线
为焦点,4为长轴长的椭圆,从而可得结果;(2)把直线![]() ,代入椭圆方程消去
,代入椭圆方程消去![]() 得:
得: ![]() ,根据韦达定理、弦长公式 及点到直线的距离公式、三角形面积公式可将
,根据韦达定理、弦长公式 及点到直线的距离公式、三角形面积公式可将![]() 的面积表示为关于
的面积表示为关于![]() 的函数,利用基本不等式求最值即可.
的函数,利用基本不等式求最值即可.
试题解析:(1)由题意知圆![]() 的圆心为
的圆心为![]() ,半径为4,
,半径为4,
所以![]() ,
,
由椭圆的定义知,动点![]() 的轨迹是以
的轨迹是以![]() 为焦点,4为长轴长的椭圆,
为焦点,4为长轴长的椭圆,
设椭圆![]() 的方程为
的方程为![]() (
(![]() ),且焦距为
),且焦距为![]()
![]() ,则:
,则:
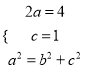 ,即
,即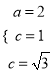 ,
,
故椭圆![]() 的方程为
的方程为![]() ;
;
(2)把直线![]() ,
,
代入椭圆方程消去![]() 得:
得: ![]() ,
,
由![]() 得:
得: ![]() 或
或![]() ,
,
因为直线与椭圆相交于两点![]() ,
, ![]() ,
,
则![]() ,
, ![]() ,
,
因为点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]()
![]() 的面积
的面积
![]()
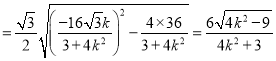
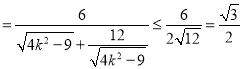 ,
,
当且仅当![]() ,即
,即![]() 时取等号,
时取等号,
![]() 满足
满足![]()
所心![]() 面积的取值范围是
面积的取值范围是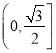 .
.
【方法点晴】本题主要考查待定系数法求椭圆方程及圆锥曲线求范围,属于难题.解决圆锥曲线中的范围问题一般有两种方法:一是几何意义,特别是用圆锥曲线的定义和平面几何的有关结论来解决,非常巧妙;二是将圆锥曲线中最值问题转化为函数问题,然后根据函数的特征选用参数法、配方法、判别式法、三角函数有界法、函数单调性法以及均值不等式法,本题(2)就是用的这种思路,利用均值不等式法求三角形范围的.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某书店销售刚刚上市的某知名品牌的高三数学单元卷,按事先拟定的价格进行5天试销,每种单价试销1天,得到如表数据:
单价x(元) | 18 | 19 | 20 | 21 | 22 |
销量y(册) | 61 | 56 | 50 | 48 | 45 |
(1)求试销5天的销量的方差和y对x的回归直线方程;
(2)预计今后的销售中,销量与单价服从(1)中的回归方程,已知每册单元卷的成本是14元,
为了获得最大利润,该单元卷的单价应定为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣lnx.
(1)求曲线f(x)在点(1,f(1))处的切线方程;
(2)求函数f(x)的单调递减区间:
(3)设函数g(x)=f(x)﹣x2+ax,a>0,若x∈(O,e]时,g(x)的最小值是3,求实数a的值.(e为自然对数的底数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是等边三角形,边长为4,
是等边三角形,边长为4, ![]() 边的中点为
边的中点为![]() ,椭圆
,椭圆![]() 以
以![]() ,
, ![]() 为左、右两焦点,且经过
为左、右两焦点,且经过![]() 、
、![]() 两点。
两点。
(1)求该椭圆的标准方程;
(2)过点![]() 且
且![]() 轴不垂直的直线
轴不垂直的直线![]() 交椭圆于
交椭圆于![]() ,
, ![]() 两点,求证:直线
两点,求证:直线![]() 与
与![]() 的交点在一条定直线上.
的交点在一条定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(Ⅰ)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设曲线![]() 经过伸缩变换
经过伸缩变换 得到曲线
得到曲线![]() ,若点
,若点![]() ,直线
,直线![]() 与
与![]() 交与
交与![]() ,
, ![]() ,求
,求![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某地区儿童的身高与体重的一组数据,我们用两种模型①![]() ,②
,②![]() 拟合,得到回归方程分别为
拟合,得到回归方程分别为![]() ,
, ![]() ,作残差分析,如表:
,作残差分析,如表:
身高 | 60 | 70 | 80 | 90 | 100 | 110 |
体重 | 6 | 8 | 10 | 14 | 15 | 18 |
| 0.41 | 0.01 | 1.21 | -0.19 | 0.41 | |
| -0.36 | 0.07 | 0.12 | 1.69 | -0.34 | -1.12 |
(Ⅰ)求表中空格内的值;
(Ⅱ)根据残差比较模型①,②的拟合效果,决定选择哪个模型;
(Ⅲ)残差大于![]() 的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.
的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.
(结果保留到小数点后两位)
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为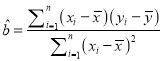 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱ABOA′B′O′中,∠AOB=90°,侧棱OO′⊥面OAB,OA=OB=OO′=2.若C为线段O′A的中点,在线段BB′上求一点E,使|EC|最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com