
【题目】如图几何体是圆锥的一部分,它是Rt△ABC(及其内部)以一条直角边AB所在直线为旋转轴旋转150°得到的,AB=BC=2,P是弧![]() 上一点,且EB⊥AP.
上一点,且EB⊥AP.
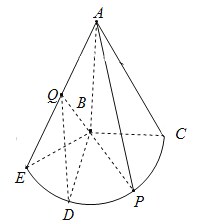
(1)求∠CBP的大小;
(2)若Q为AE的中点,D为弧![]() 的中点,求二面角Q﹣BD﹣P的余弦值;
的中点,求二面角Q﹣BD﹣P的余弦值;
(3)直线AC上是否存在一点M,使得B、D、M、Q四点共面?若存在,请说明点M的位置;若不存在,请说明理由.
【答案】(1)60°(2)![]() (3)存在;直线AC与平面BQD相交,交点为所求点M
(3)存在;直线AC与平面BQD相交,交点为所求点M
【解析】
(1)根据线面垂直推出线线垂直,结合已知角度的大小,即可求得;
(2)根据二面角的定义,作出二面角的补角,求得该补角后,再求出原二面角大小即可.
(3)假设![]() 与平面
与平面![]() 平行,推证矛盾,再说明点
平行,推证矛盾,再说明点![]() 所在位置即为直线与平面的交点即可.
所在位置即为直线与平面的交点即可.
(1)∵AB⊥平面BEC,∴AB⊥BE,
又EB⊥AP,AB∩AP=A,
∴BE⊥平面ABP,则EB⊥BP,
又∠EBC=150°
∴∠CBP=60°;
(2)过Q作QF⊥BE,垂直为F,则QF⊥平面BEC,
过F作FG⊥BD,垂直为G,连接QG,如下图所示:
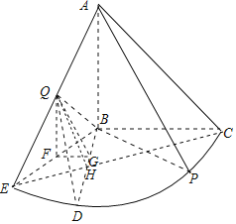
则∠QGF为二面角Q﹣BD﹣E的平面角,
∵D为弧EP的中点,∴∠FBG=45°,
∵Q是AE的中点,∴QF![]() ,
,
因为QF⊥BE,![]() ,故可得
,故可得![]() //
//![]() ,
,
则点![]() 也是
也是![]() 的中点,故BF
的中点,故BF![]()
![]() ,
,
因为QF⊥BE,![]() ,故可得
,故可得![]() //
//![]() ,
,
则点![]() 也是
也是![]() 的中点,故BF
的中点,故BF![]() ,
,
在![]() 中,
中,![]() .
.
因为![]() //
//![]() ,
,![]() 平面
平面![]() ,故可得
,故可得![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,故可得
,故可得![]()
则在![]() 中,
中,
则在Rt△QGF中,可得cos∠QGF![]() ,
,
因为二面角Q﹣BD﹣P的平面角与二面角Q﹣BD﹣E的平面角互补,
∴二面角Q﹣BD﹣P的余弦值为![]() ;
;
(3)直线AC上存在一点M,使得B、D、M、Q四点共面.
事实上,若直线AC与平面BQD相交,则交点为所求点M.
下面说明直线AC与平面BQD相交:
若AC∥平面BQD,
连接EC,交平面BQD于H,
连接QH,则QH∥AC.
∵Q为AE的中点,则H为EC中点,
由∠EBD=45°,∠CBD=105°,
可知H不是EC中点,矛盾.
∴直线AC与平面BQD相交,交点为所求点M.
即直线AC上存在一点M,使得B、D、M、Q四点共面,
该点为直线AC与平面BQD的交点.


科目:高中数学 来源: 题型:
【题目】设min{m,n}表示m,n二者中较小的一个,已知函数f(x)=x2+8x+14,g(x)=![]() (x>0),若x1∈[-5,a](a≥-4),x2∈(0,+∞),使得f(x1)=g(x2)成立,则a的最大值为
(x>0),若x1∈[-5,a](a≥-4),x2∈(0,+∞),使得f(x1)=g(x2)成立,则a的最大值为
A.-4B.-3C.-2D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为![]() .
.
(1)求sinBsinC;
(2)若3cosB(sin2A+sin2B﹣sin2C)=sinAsinB,a=6,求b+c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的个数有( )
(1)在空间直角坐标系中,点![]() 关于平面
关于平面![]() 的对称点为
的对称点为![]() ,则点
,则点![]() 关于原点的对称点
关于原点的对称点![]() 的坐标为
的坐标为![]() .
.
(2)![]() .
.
(3)1908和4187的最大公约数是53.
(4)用秦九韶算法计算多项式![]() ,当
,当![]() 时的值
时的值![]() .
.
(5)古代“五行”学说认为:“物质分金,木,土,水,火五种属性,金克木,木克土,土克水,水克火,火克金.”将五种不同属性的物质任意排成一列,设事件A表示“排列中属性相克的两种物质不相邻”,则事件A的概率为![]() .
.
A.2B.3C.4D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高二全体师生今秋开学前在新校区体验周活动中有优异的表现,学校拟对高二年级进行表彰;
(1)若要表彰3个优秀班级,规定从6个文科班中选一个,14个理科班中选两个班级,有多少种不同的选法?
(2)年级组拟在选出的三个班级中再选5名学生,每班至少1名,最多2名,则不同的分配方案有多少种?
(3)选中的这5名学生和三位年级负责人徐主任,陈主任,付主任排成一排合影留念,规定这3位老师不排两端,且老师顺序固定不变,那么不同的站法有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知点
轴的正半轴为极轴建立极坐标系,已知点![]() 的直角坐标为
的直角坐标为![]() ,若直线
,若直线![]() 的极坐标方程为
的极坐标方程为![]() 曲线
曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)求直线![]() 和曲线
和曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com