
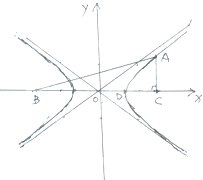
如图,直角坐标系xOy中,Rt△ABC中∠C=90°,B、C在x轴上且关于原点O对称,D在边BC上,BD=3DC,△ABC的周长为12.若一双曲线E以B、C为焦点,且经过A、D两点。
(1)求双曲线的方程;
(2)若过点P(m,0)(m为非零常数)的直线L与双曲线E相交于不同于双曲线顶点的两点M、N,且 ,问x轴上是否存在定点G,使
,问x轴上是否存在定点G,使 ?若存在,求出所有这样定点G的坐标;若不存在,请说明理由。
?若存在,求出所有这样定点G的坐标;若不存在,请说明理由。
 |
解:(1)设双曲线E的方程为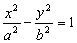 (a>0, b>0),则B(-c,0),D(c,0),C(c,0)
(a>0, b>0),则B(-c,0),D(c,0),C(c,0)
由BD=3DC,得c+a=3(c-a),即c=2a
∴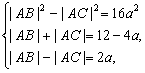 解之得a=1, ∴c=2,b=
解之得a=1, ∴c=2,b=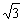
∴双曲线E的方程为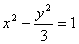
(2)如图,设在x轴上存在定点G(t,0),使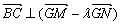
设直线l的方程为x-m=ky, M(x1,y1)、N(x2,y2)
由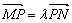 ,得y1+λy2=0,即
,得y1+λy2=0,即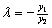 ①
①
∵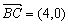 ,
,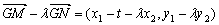 ,
,
∴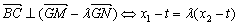
即ky1+m-t=λ(ky2+m-t) ②
把①代入②得 2ky1y2+(m-t)(y1+y2)=0③
把x-m=ky代入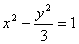 并整理得(3k)y2+6kmy+3(m)=0,
并整理得(3k)y2+6kmy+3(m)=0,
其中3k≠0且△>0
即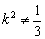 且3k2+m2>1
且3k2+m2>1
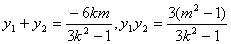 ,代入③得
,代入③得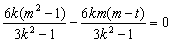
化简得kmt=t.当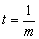 时,上式恒成立。
时,上式恒成立。
因此,在x轴上存在定点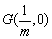 ,使
,使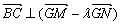 。
。


科目:高中数学 来源: 题型:
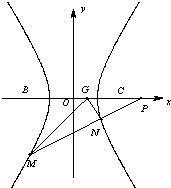
 如图,直角坐标系xoy中,有Rt△ABC,∠C=90°,D在边BC上,BD=3DC,双曲线E以B、C为焦点,且经过A、D两点.
如图,直角坐标系xoy中,有Rt△ABC,∠C=90°,D在边BC上,BD=3DC,双曲线E以B、C为焦点,且经过A、D两点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,直角坐标系xOy中,一直角三角形ABC,∠C=90°,B、C在x轴上且关于原点O对称,D在边BC上,BD=3DC,△ABC的周长为12.若一双曲线E以B、C为焦点,且经过A、D两点.
如图,直角坐标系xOy中,一直角三角形ABC,∠C=90°,B、C在x轴上且关于原点O对称,D在边BC上,BD=3DC,△ABC的周长为12.若一双曲线E以B、C为焦点,且经过A、D两点.| MP |
| PN |
| BC |
| GM |
| GN |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•芜湖二模)如图,直角坐标系XOY中,点F在x轴正半轴上,△OFG的面积为S.且
(2012•芜湖二模)如图,直角坐标系XOY中,点F在x轴正半轴上,△OFG的面积为S.且| OF |
| FG |
| OF |
| 3 |
| 4 |
| OG |
| AP |
| CD |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•蓝山县模拟)如图,直角坐标系xOy中,一直角三角形ABC,∠=90°,B、C在x轴上且关于原点O对称,D在边BC上,BD=3DC,△ABC的周长为12.若一双曲线E以B、C为焦点,且经过A、D两点.
(2012•蓝山县模拟)如图,直角坐标系xOy中,一直角三角形ABC,∠=90°,B、C在x轴上且关于原点O对称,D在边BC上,BD=3DC,△ABC的周长为12.若一双曲线E以B、C为焦点,且经过A、D两点.| MP |
| PN |
| BC |
| GM |
| GN |
查看答案和解析>>
科目:高中数学 来源: 题型:
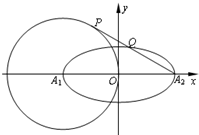 如图平面直角坐标系xOy中,椭圆
如图平面直角坐标系xOy中,椭圆| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| PQ |
| QA2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com