练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设函数f(x)＝ax2＋bx＋b－1(a≠0)．

    (1)当a＝1，b＝－2时，求函数f(x)的零点；

    (2)若对任意b∈R，函数f(x)恒有两个不同零点，求实数a的取值范围．

     

    (1) 3和－1 (2) (0,1)

    【解析】(1)当a＝1，b＝－2时，f(x)＝x2－2x－3，

    令f(x)＝0，得x＝3或x＝－1.

    ∴函数f(x)的零点为3和－1.

    (2)依题意，f(x)＝ax2＋bx＋b－1＝0有两个不同实根．

    ∴b2－4a(b－1)＞0恒成立，

    即对于任意b∈R，b2－4ab＋4a＞0恒成立，

    所以有(－4a)2－4(4a)＜0⇒a2－a＜0，所以0＜a＜1.

    因此实数a的取值范围是(0,1)．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学（文）二轮专题复习与测试专题2第3课时练习卷（解析版） 题型：填空题

    在△ABC中，AB＝10，AC＝6，O为BC的垂直平分线上一点，则·＝________.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（文）二轮专题复习与测试专题1第6课时练习卷（解析版） 题型：解答题

    已知a∈R，函数f(x)＝4x3－2ax＋a.

    (1)求f(x)的单调区间；

    (2)证明：当0≤x≤1时，f(x)＋|2－a|＞0.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（文）二轮专题复习与测试专题1第4课时练习卷（解析版） 题型：解答题

    设集合A＝{x|x2＜4}，B＝.

    (1)求集合A∩B；

    (2)若不等式2x2＋ax＋b＜0的解集为B，求a，b的值．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（文）二轮专题复习与测试专题1第4课时练习卷（解析版） 题型：选择题

    设P和Q是两个集合，定义集合P－Q＝{x|x∈P，且x∉Q}，如果P＝{x|log2x＜1}，Q＝{x||x－2|＜1}，那么P－Q等于(　　)

    A．{x|0＜x＜1} B．{x|0＜x≤1}

    C．{x|1＜x＜2} D．{x|2＜x＜3}

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（文）二轮专题复习与测试专题1第3课时练习卷（解析版） 题型：选择题

    如果一个点是一个指数函数和一个对数函数的图象的交点，那么称这个点为“好点”．下列四个点P1(1，1)，P2(1,2)，P3，P4(2,2)中，“好点”的个数为(　　)

    A．1 B．2

    C．3 D．4

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（文）二轮专题复习与测试专题1第2课时练习卷（解析版） 题型：填空题

    对于定义在R上的函数f(x)有以下五个命题：

    ①若y＝f(x)是奇函数，则y＝f(x－1)的图象关于A(1,0)对称；

    ②若对于任意x∈R，有f(x－1)＝f(x＋1)，则f(x)关于直线x＝1对称；

    ③函数y＝f(x＋1)与y＝f(1－x)的图象关于直线x＝1对称；

    ④如果函数y＝f(x)满足f(x＋1)＝f(1－x)，f(x＋3)＝f(3－x)，那么该函数以4为周期．

    其中正确命题的序号为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（文）二轮专题复习与测试专题1第1课时练习卷（解析版） 题型：选择题

    下列命题中正确的是(　　)

    A．若命题p为真命题，命题q为假命题，则命题“p∧q”为真命题

    B．“sinα＝”是“α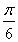＝的充分不必要条件”

    C．l为直线，α，β为两个不同的平面，若l⊥β，α⊥β，则l∥α

    D．命题“?x∈R,2x＞0”的否定是“?x0∈R,2x0≤0”

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学理复习方案二轮作业手册新课标·通用版专题八练习卷（解析版） 题型：解答题

    已知向量p＝(an，2n)，q＝(2n＋1，－an＋1)，n∈N*，p与q垂直，且a1＝1.

    (1)求数列{an}的通项公式；

    (2)若数列{bn}满足bn＝log2an＋1，求数列{an·bn}的前n项和Sn.

     

    查看答案和解析>>

    同步练习册答案