
【题目】已知a为实数,f(x)=(x2﹣4)(x﹣a).
(1)求导数f′(x);
(2)若f′(﹣1)=0,求f(x)在[﹣2,2]上的最大值和最小值.
【答案】
(1)解:∵f(x)=(x2﹣4)(x﹣a)
=x3﹣ax2﹣4x+4a,
∴f′(x)=3x2﹣2ax﹣4.
(2)解:∵f'(﹣1)=3+2a﹣4=0,
∴a= ![]() .f(x)=(x2﹣4)(x﹣
.f(x)=(x2﹣4)(x﹣ ![]() )
)
∴由f′(x)=3x2﹣x﹣4=0,
得x1=﹣1, ![]() ,
,
∵ ![]() =0,
=0,
![]() =
= ![]() ,
,
![]() =﹣
=﹣ ![]() ,
,
![]() .
.
∴f(x)在[﹣2,2]上的最大值为 ![]() ,
,
最小值为﹣ ![]()
【解析】(1)f(x)=(x2﹣4)(x﹣a)=x3﹣ax2﹣4x+4a,能求出导数f′(x);(2)由f'(﹣1)=3+2a﹣4=0,得a= ![]() .由f′(x)=3x2﹣x﹣4=0,得x1=﹣1,
.由f′(x)=3x2﹣x﹣4=0,得x1=﹣1, ![]() ,然后分别求出
,然后分别求出 ![]() 和f(2),由此能得到f(x)在[﹣2,2]上的最大值和最小值.
和f(2),由此能得到f(x)在[﹣2,2]上的最大值和最小值.
【考点精析】利用函数的最大(小)值与导数对题目进行判断即可得到答案,需要熟知求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项为Sn , 点(n, ![]() ),(n∈N*)均在函数y=3x﹣2的图象上.
),(n∈N*)均在函数y=3x﹣2的图象上.
(1)求数列{an}的通项公式.
(2)设bn= ![]() ,Tn为数列{bn}的前n项和,求使得Tn<
,Tn为数列{bn}的前n项和,求使得Tn< ![]() 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ),x∈R(其中 ![]() )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为 ![]() ,且图象上一个最低点为
,且图象上一个最低点为 ![]() . (Ⅰ)求f(x)的解析式;
. (Ⅰ)求f(x)的解析式;
(Ⅱ)当 ![]() ,求f(x)的值域.
,求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)的图象经过点 ![]() . (Ⅰ)求函数f(x)的解析式;
. (Ⅰ)求函数f(x)的解析式;
(Ⅱ)判断函数f(x)在区间(0,+∞)上的单调性,并用单调性的定义证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=ax3﹣3x+1 对于x∈[﹣1,1]总有f(x)≥0成立,则a 的取值范围为( )
A.[2,+∞)
B.[4,+∞)
C.{4}
D.[2,4]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一个半径适当的小球放入如图所示的容器自上方的入口处,小球自由下落,小气在下落的过程中,将遇到黑色障碍物3次,最后落入A袋或B袋中,已知小球每次遇到障碍物时,向左、右两边下落的概率分别是 ![]() ,
, ![]()
(1)分别求出小球落入A袋和B袋中的概率;
(2)在容器 入口处依次放入4个小球,记ξ为落入B袋中的小球个数,求ξ的分布列和数学期望.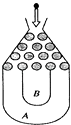
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com