
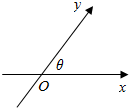
 如图,数轴x,y的交点为O,夹角为θ,与x轴、y轴正向同向的单位向量分别是$\overrightarrow{e_1},\overrightarrow{e_2}$.由平面向量基本定理,对于平面内的任一向量$\overrightarrow{OP}$,存在唯一的有序实数对(x,y),使得$\overrightarrow{OP}=x\overrightarrow{e_1}+y\overrightarrow{e_2}$,我们把(x,y)叫做点P在斜坐标系xOy中的坐标(以下各点的坐标都指在斜坐标系xOy中的坐标).
如图,数轴x,y的交点为O,夹角为θ,与x轴、y轴正向同向的单位向量分别是$\overrightarrow{e_1},\overrightarrow{e_2}$.由平面向量基本定理,对于平面内的任一向量$\overrightarrow{OP}$,存在唯一的有序实数对(x,y),使得$\overrightarrow{OP}=x\overrightarrow{e_1}+y\overrightarrow{e_2}$,我们把(x,y)叫做点P在斜坐标系xOy中的坐标(以下各点的坐标都指在斜坐标系xOy中的坐标).分析 (1)设出P点坐标,结合$\overrightarrow{OP}$为单位向量,且$\overrightarrow{OP}$与$\overrightarrow{e_1}$的夹角为120°列式求解;
(2)由题意求出$|\overrightarrow{OP}|$,$\overrightarrow{OP}•\overrightarrow{{e}_{1}}$,代入数量积求夹角公式得答案;
(3)由题意得到A在直角坐标系和斜坐标系下坐标的关系,求出直角坐标系下名字条件的直线方程,转化为斜坐标系下得答案.
解答 解:(1)若θ=90°,$\overrightarrow{OP}$为单位向量,且$\overrightarrow{OP}$与$\overrightarrow{e_1}$的夹角为120°,
设P(x,y),则x2+y2=1,且cos120°=($x\overrightarrow{{e}_{1}}+y\overrightarrow{{e}_{2}}$)$•\overrightarrow{{e}_{1}}$=x,
∴x=-$\frac{1}{2}$,代入x2+y2=1,得y=$±\frac{\sqrt{3}}{2}$.
可得P$({-\frac{1}{2},±\frac{{\sqrt{3}}}{2}})$;
(2)若θ=45°,点P的坐标为$({1,\sqrt{2}})$,则$\overrightarrow{OP}=\overrightarrow{{e}_{1}}+\sqrt{2}\overrightarrow{{e}_{2}}$,
∴$|\overrightarrow{OP}{|}^{2}=(\overrightarrow{{e}_{1}}+\sqrt{2}\overrightarrow{{e}_{2}})^{2}=|\overrightarrow{{e}_{1}}{|}^{2}+2\sqrt{2}|\overrightarrow{{e}_{1}}||\overrightarrow{{e}_{2}}|cos45°$$+2|\overrightarrow{{e}_{2}}{|}^{2}$=$1+2\sqrt{2}×\frac{\sqrt{2}}{2}+2=5$,
∴$|\overrightarrow{OP}|=\sqrt{5}$,
又$\overrightarrow{OP}•\overrightarrow{{e}_{1}}=(\overrightarrow{{e}_{1}}+\sqrt{2}\overrightarrow{{e}_{2}})•\overrightarrow{{e}_{1}}=|\overrightarrow{{e}_{1}}{|}^{2}$$+\sqrt{2}|\overrightarrow{{e}_{1}}||\overrightarrow{{e}_{2}}|cos45°$=$1+\sqrt{2}×\frac{\sqrt{2}}{2}=2$,
设向量$\overrightarrow{OP}$与$\overrightarrow{e_1}$的夹角为α,则$cosα=\frac{\overrightarrow{OP}•\overrightarrow{{e}_{1}}}{|\overrightarrow{OP}||\overrightarrow{{e}_{1}}|}$=$\frac{2}{\sqrt{5}×1}=\frac{2\sqrt{5}}{5}$.
∴α=$arccos\frac{{2\sqrt{5}}}{5}$;
(3)若θ=60°,且点A(2,1),
由$x=x′+\frac{1}{2}y′,y=\frac{\sqrt{3}}{2}y′$,可得A在直角坐标系下的坐标为($\frac{5}{2},\frac{\sqrt{3}}{2}$),
∴过点A($\frac{5}{2},\frac{\sqrt{3}}{2}$)且使得原点O到直线l的距离最大的直线方程为$y-\frac{\sqrt{3}}{2}=-\frac{5}{\sqrt{3}}(x-\frac{5}{2})$,
代入$x=x′+\frac{1}{2}y′,y=\frac{\sqrt{3}}{2}y′$,整理得5x′+4y′-14=0.
∴过点A(2,1),使得原点O到直线l的距离最大的直线方程为5x+4y-14=0.
点评 本题考查平面向量的数量积运算,关键是对题意的理解,属中档题.


科目:高中数学 来源: 题型:选择题
| 型号 | 小包装 | 大包装 |
| 重量 | 100克 | 300克 |
| 包装费 | 0.5元 | 0.7元 |
| 销售价格 | 3.00元 | 8.4元 |
| A. | ①② | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=3或4 | B. | x=±3或4 | C. | x=-3或4 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2π-9 | B. | 9-2π | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,2$\sqrt{2}$] | B. | [4,8] | C. | [-2,2] | D. | [0,2$\sqrt{2}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com