
某高校共有学生15 000人,其中男生10 500人,女生4 500人,为调查该校学生每周平均体育运动的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为:[0,2],(2,4], (4,6], (6,8], (8,10], (10,12],估计该校学生每周平均体育运动时间超过4小时的概率;
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
附:

| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
(1) 90;(2) 0.75;(3) 有.
解析试题分析:(1)由分层抽样方法可知每层应抽取的比例相同且为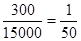 ,所以女生应抽取人数就等于女生总人数4 500 乘以抽取比例;(2) 该校学生每周平均体育运动时间超过4小时的概率等于1减去[0,2],(2,4]矩形方块的高度之和乘以组距2; (3)首先应计算出在样本数据的300人中,每周平均体育运动时间超过4小时的男生人数和女生人数,列出
,所以女生应抽取人数就等于女生总人数4 500 乘以抽取比例;(2) 该校学生每周平均体育运动时间超过4小时的概率等于1减去[0,2],(2,4]矩形方块的高度之和乘以组距2; (3)首先应计算出在样本数据的300人中,每周平均体育运动时间超过4小时的男生人数和女生人数,列出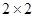 列联表,然后根据公式计算出
列联表,然后根据公式计算出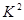 的观测值,如果
的观测值,如果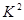 的观测值大于3.841,则就有有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”;否则就没有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
的观测值大于3.841,则就有有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”;否则就没有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
试题解析:(1) 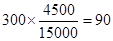 ,所以应收集90位女生的样本数据。
,所以应收集90位女生的样本数据。
(2)由频率分布直方图得1-2×(0.100+0.025)=0.75,所以该校学生每周平均体育运动时间超过4小时的概率的估计值为0.75。
(3)由(2)知,300位学生中有300×0.75=225人的每周平均体育运动时间超过4小时,75人的每周平均体育运动时间不超过4小时,又因为样本数据中有210份是关于男生的,90份是关于女生的,所以每周平均体育运动时间与性别列联表如下:
每周平均体育运动时间与性别列联表。 男生 女生 总计 每周平均体育运动时间
不超过4小时45 30 75 每周平均体育运动时间
超过4小时165 60 225 总计 210 90 300
结合列联表可算得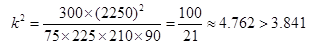 .所以,有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
.所以,有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
考点:1.分层抽样;2. 频率分布直方图;3.独立性检验.


科目:高中数学 来源: 题型:解答题
某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)
(1)应收集多少位女生样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为: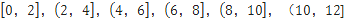 .估计该校学生每周平均体育运动时间超过4个小时的概率.
.估计该校学生每周平均体育运动时间超过4个小时的概率.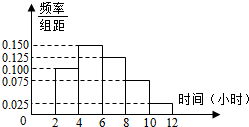
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4个小时.请完成每周平均体育运动时间与性别的列联表,并判断是否有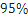 的把握认为“该校学生的每周平均体育运动时间与性别有关”.
的把握认为“该校学生的每周平均体育运动时间与性别有关”.
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
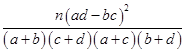
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
随机抽取某中学甲班10名同学,他们的身高(单位:cm)数据是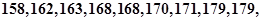
 ;乙班10名同学,他们的身高(单位:cm)数据是
;乙班10名同学,他们的身高(单位:cm)数据是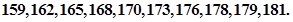
(1)画出甲、乙两班的茎叶图,并说明茎叶图有什么优点和缺点?
(2)根据茎叶图判断哪个班的平均身高较高(不必计算).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
由散点图可知,销售量 与价格
与价格 之间有较好的线性相关关系,其线性回归直线方程是;
之间有较好的线性相关关系,其线性回归直线方程是;
(1)求 的值;
的值;
(2)预计在今后的销售中,销量与单价仍然服从线性回归直线方程中的关系,且该产品的成本是每件4元,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入一成本)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知某单位有50名职工,现要从中抽取10名职工,将全体职工随机按1~50编号,并按编号顺序平均分成10组,按各组内抽取的编号依次增加5进行系统抽样.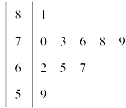
(1)若第5组抽出的号码为22,写出所有被抽出职工的号码;
(2)分别统计这10名职工的体重(单位:公斤),获得体重数据的茎叶图如图所示,求该样本的方差;
(3)在(2)的条件下,从这10名职工中随机抽取两名体重不轻于73公斤(≥73公斤)的职工,求体重为76公斤的职工被抽取到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某化肥厂甲、乙两个车间包装肥料,在自动包装传送带上每隔30 min抽取一包产品,称其重量,分别记录抽查数据如下:
甲:102,101,99,98,103,98,99;
乙:110,115,90,85,75,115,110.
(1)这种抽样方法是哪一种?
(2)将这两组数据用茎叶图表示;
(3)将两组数据比较,说明哪个车间的产品较稳定.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
小区统计部门随机抽查了区内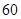 名网友4月1日这天的网购情况,得到如下数据统计表(图(1)).网购金额超过
名网友4月1日这天的网购情况,得到如下数据统计表(图(1)).网购金额超过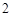 千元的顾客被定义为“网购红人”,网购金额不超过
千元的顾客被定义为“网购红人”,网购金额不超过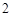 千元的顾客被定义为“非网购红人”.已知“非网购红人”与“网购红人”人数比恰为
千元的顾客被定义为“非网购红人”.已知“非网购红人”与“网购红人”人数比恰为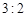 .
.
(1)确定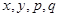 的值,并补全频率分布直方图(图(2)).
的值,并补全频率分布直方图(图(2)).
(2)为进一步了解这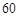 名网友的购物体验,从“非网购红人”和“网购红人”中用分层抽样的方法确定
名网友的购物体验,从“非网购红人”和“网购红人”中用分层抽样的方法确定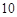 人,若需从这
人,若需从这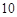 人中随机选取
人中随机选取 人进行问卷调查,设
人进行问卷调查,设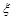 为选取的
为选取的 人中“网购红人”的人数,求
人中“网购红人”的人数,求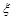 的分布列和数学期望.
的分布列和数学期望.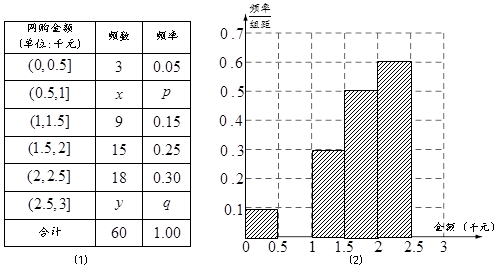
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
某市高三数学抽样考试中,对90分以上
(含90分)的成绩进行统计,其频率分布图
如图所示,若130—140分数段的人数为90人,
则90—100分数段的人数为_______
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com