
【题目】已知a为实数,若函数f(x)=|x2+ax+2|﹣x2在区间(﹣∞,﹣1)和(2,+∞)上单调递减,则实数a的取值范围为 .
【答案】[﹣8,0)
【解析】解:f(x)=|x2+ax+2|﹣x2= ![]() ,
,
设x2+ax+2=0的两个根分别为x1 , x2 , (x1<x2),
则f(x)= ![]() ,
,
∵当x≥x2时,函数f(x)=ax+2,函数f(x)在(2,+∞)上单调递减,
∴a<0,
当x1<x<x2时,抛物线的对称轴为x=﹣ ![]() =﹣
=﹣ ![]() .
.
若函数f(x)在(2,+∞)上单调递减,则﹣ ![]() ≤2,得﹣8≤a<0.
≤2,得﹣8≤a<0.
若f(x)在区间(﹣∞,﹣1)递减,
则x1= ![]() ≥﹣1,
≥﹣1,
即﹣a﹣ ![]() ≥﹣2,
≥﹣2,
则 ![]() ≥a﹣2,
≥a﹣2,
∵﹣8≤a<0,
∴ ![]() ≥a﹣2恒成立,
≥a﹣2恒成立,
综上﹣8≤a<0,
所以答案是:[﹣8,0)
【考点精析】掌握函数的单调性是解答本题的根本,需要知道注意:函数的单调性是函数的局部性质;函数的单调性还有单调不增,和单调不减两种.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】已知某中学联盟举行了一次“盟校质量调研考试”活动,为了解本次考试学生的某学科成绩情况,从中抽取部分学生的分数(满分为![]() 分,得分取正整数,抽取学生的分数均在
分,得分取正整数,抽取学生的分数均在![]() 之内)作为样本(样本容量为
之内)作为样本(样本容量为![]() )进行统计,按照
)进行统计,按照![]() 的分组作出频率分布直方图,并作出样本分数的茎叶图(茎叶图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(茎叶图中仅列出了得分在![]() 的数据)
的数据)
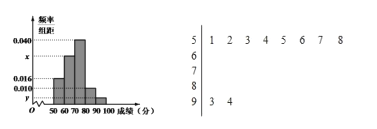
(Ⅰ)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(Ⅱ)在选取的样本中,从成绩在![]() 分以上(含
分以上(含![]() 分)的学生中随机抽取
分)的学生中随机抽取![]() 名学生参加“省级学科基础知识竞赛”,求所抽取的
名学生参加“省级学科基础知识竞赛”,求所抽取的![]() 名学生中恰有一人得分在
名学生中恰有一人得分在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]()
(1)求函数 ![]() 的定义域;
的定义域;
(2)若存在a∈R,对任意 ![]() ,总存在唯一x0∈[﹣1,2],使得f(x1)=g(x0)成立.求实数a的取值范围.
,总存在唯一x0∈[﹣1,2],使得f(x1)=g(x0)成立.求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】请先阅读:
在等式cos2x=2cos2x﹣1(x∈R)的两边求导,得:(cos2x)′=(2cos2x﹣1)′,由求导法则,得(﹣sin2x)2=4cosx(﹣sinx),化简得等式:sin2x=2cosxsinx.
(1)利用上题的想法(或其他方法),结合等式(1+x)n=Cn0+Cn1x+Cn2x2+…+Cnnxn(x∈R,正整数n≥2),证明: ![]() .
.
(2)对于正整数n≥3,求证:
(i) ![]() ;
;
(ii) ![]() ;
;
(iii) ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋装有大小相同的小球9个,其中红球2个、黑球3个、白球4个,现从中抽取2次,每次抽取一个球.
(1)若有放回地抽取2次,求两次所取的球的颜色不同的概率;
(2)若不放回地抽取2次,取得红球记2分,取得黑球记1分,取得白球记0分,记两次取球的得分之和为随机变量X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0且a≠1,函数f(x)=loga(x+1), ![]() ,记F(x)=2f(x)+g(x)
,记F(x)=2f(x)+g(x)
(1)求函数F(x)的定义域D及其零点;
(2)试讨论函数F(x)在定义域D上的单调性;
(3)若关于x的方程F(x)﹣2m2+3m+5=0在区间[0,1)内仅有一解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知Sn是等差数列{an}的前n项和,且a2=2,S5=15.
(1)求通项公式an;
(2)若数列{bn}满足bn=2an﹣an , 求{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个函数:
①y=3﹣x;②y=2x﹣1(x>0);③y=x2+2x﹣10,;④ 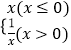 .
.
其中定义域与值域相同的函数有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com