
【题目】已知椭圆![]() :
:![]() 过点
过点 和点
和点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,
, ![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() ?若存在,求出实数
?若存在,求出实数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】已知数集![]() 具有性质
具有性质![]() :对任意的
:对任意的![]()
![]() ,
,![]() ,使得
,使得![]() 成立.
成立.
(Ⅰ)分别判断数集![]() 与
与![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(Ⅱ)求证![]() ;
;
(Ⅲ)若![]() ,求数集
,求数集![]() 中所有元素的和的最小值.
中所有元素的和的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2019年春运期间十二个城市售出的往返机票的平均价格以及相比去年同期变化幅度的数据统计图,给出下列4个结论
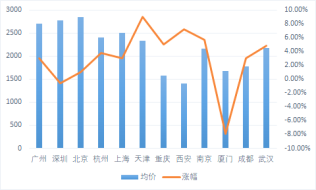
其中结论正确的是( )
A.深圳的变化幅度最小,北京的平均价格最高;
B.深圳和厦门往返机票的平均价格同去年相比有所下降;
C.平均价格从高到低位于前三位的城市为北京,深圳,广州;
D.平均价格的涨幅从高到低位于前三位的城市为天津,西安,上海.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某单位的食堂中,食堂每天以![]() 元/斤的价格购进米粉,然后以4.4元/碗的价格出售,每碗内含米粉0.2斤,如果当天卖不完,剩下的米粉以2元/斤的价格卖给养猪场.根据以往统计资料,得到食堂某天米粉需求量的频率分布直方图如图所示,若食堂某天购进了80斤米粉,以
元/斤的价格购进米粉,然后以4.4元/碗的价格出售,每碗内含米粉0.2斤,如果当天卖不完,剩下的米粉以2元/斤的价格卖给养猪场.根据以往统计资料,得到食堂某天米粉需求量的频率分布直方图如图所示,若食堂某天购进了80斤米粉,以![]() (单位:斤)(其中
(单位:斤)(其中![]() )表示米粉的需求量,
)表示米粉的需求量, ![]() (单位:元)表示利润.
(单位:元)表示利润.
(Ⅰ)计算当天米粉需求量的平均数,并直接写出需求量的众数和中位数;
(Ⅱ) 将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅲ)根据直方图估计该天食堂利润不少于760元的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某市主办的科技知识竞赛的学生成绩中随机选取了40名学生的成绩作为样本,已知这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式分成6组,第一组![]() ;第二组
;第二组![]() ;…;第六组
;…;第六组![]() ,并据此绘制了如图所示的频率分布直方图.
,并据此绘制了如图所示的频率分布直方图.
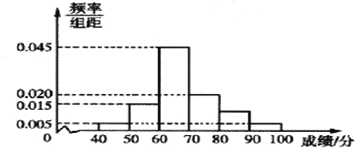
(1)求成绩在区间![]() 内的学生人数;
内的学生人数;
(2)从成绩大于等于80分的学生中随机选取2名,求至少有1名学生的成绩在区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是一个容量为20的样本数据分组后的频率分布表:
分组 | [8.5,11.5] | [11.5,14.5] | [14.5,17.5] | [17.5,20.5] |
频数 | 4 | 2 | 6 | 8 |
(I)若用组中值代替本组数据的平均数,请计算样本的平均数![]() ;
;
(II)以频率估计概率,若样本的容量为2000,求在分组[14.5,17.5)中的频数;
(Ⅲ)若从数据在分组[8.5,11.5)与分组[11.5,14.5)的样本中随机抽取2个,求恰有1个样本落在分组[11.5,14.5)的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均为正数的两个数列![]() 和{
和{![]() }满足:an+1=
}满足:an+1=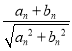 ,n∈N*.
,n∈N*.
(1)设bn+1=1+![]() ,n∈N*,求证:数列
,n∈N*,求证:数列![]() 是等差数列;
是等差数列;
(2)设bn+1=![]() ·
·![]() ,n∈N*,且
,n∈N*,且![]() 是等比数列,求a1和b1的值.
是等比数列,求a1和b1的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com