
解:(Ⅰ)过B
1C
1作底面ABCD的垂直平面,
交底面于PQ,过B
1作B
1G⊥PQ,垂足为G.
∵平面ABCD∥平面A
1B
1C
1D
1,∠A
1B
1C
1=90°
∴AB⊥PQ,AB⊥B
1P.
∴∠B
1PG为所求二面角的平面角.
过C
1作C
1H⊥PQ,垂足为H.
由于相对侧面与底面所成二面角的大小相等,
故四边形B
1PQC
1为等腰梯形.
∴

,
又B
1G=h,
∴

,
∴

,
即所求二面角的大小为

.
(Ⅱ)证明:∵AB,CD是矩形ABCD的一组对边,有AB∥CD,
又CD是面ABCD与面CDEF的交线,
∴AB∥面CDEF.
∵EF是面ABFE与面CDEF的交线,
∴AB∥EF.
∵AB是平面ABCD内的一条直线,EF在平面ABCD外,
∴EF∥面ABCD.
分析:(Ⅰ)过B
1C
1作底面ABCD的垂直平面,交底面于PQ,过B
1作B
1G⊥PQ,垂足为G,根据二面角平面角的定义可知∠B
1PG为所求二面角的平面角,过C
1作C
1H⊥PQ,垂足为H,根据相对侧面与底面所成二面角的大小相等,得到四边形B
1PQC
1为等腰梯形,在三角形B
1PG中求出此角即可.
(Ⅱ)欲证EF∥面ABCD,根据直线与平面平行的判定定理可知只需证EF与面ABCD内一直线平行即可,根据线面平行的判定定理可知AB∥面CDEF,而EF是面ABFE与面CDEF的交线,则AB∥EF,AB是平面ABCD内的一条直线,EF在平面ABCD外,满足定理所需条件.
点评:本小题主要考查直线、平面的位置关系,考查二面角的度量的基本知识,考查空间想象能力和逻辑推理能力.

 如图,在多面体ABCD-A1B1C1D1中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,侧棱延长后相交于E,F两点,上、下底面矩形的长、宽分别为c,d与a,b,且a>c,b>d,两底面间的距离为h.
如图,在多面体ABCD-A1B1C1D1中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,侧棱延长后相交于E,F两点,上、下底面矩形的长、宽分别为c,d与a,b,且a>c,b>d,两底面间的距离为h. 解:(Ⅰ)过B1C1作底面ABCD的垂直平面,
解:(Ⅰ)过B1C1作底面ABCD的垂直平面, ,
, ,
, ,
, .
.

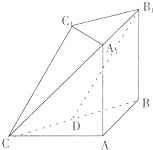 如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1
如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1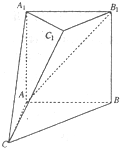 如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=
如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=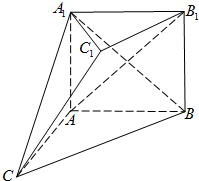 (2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,B1C1=
(2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,B1C1=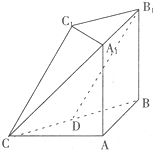 (2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1=
(2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1=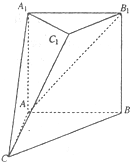 (2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=
(2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=