
(本题16分)数列{an}是等差数列,数列{bn}满足bn=anan+1an+2 (nÎN*),数列{bn}的前n项和为Sn.
(1)若数列{an}的公差d等于首项a1,试用数学归纳法证明:对于任意nÎN*,都有Sn=![]() ;
;
(2)若数列{an}满足:3a5=8a12>0,试问n为何值时,Sn取得最大值?并说明理由.
(1)当n=1时,S1=b1,![]() =
=![]() =b1,原式成立.……………………1分
=b1,原式成立.……………………1分
假设当n=k时,Sk=![]() 成立,………………………………………………2分
成立,………………………………………………2分
则Sk+1=Sk+bk+1=![]() …………………………………………………4分
…………………………………………………4分
=![]() =
=![]() =
=![]() =
=![]() ……6分
……6分
所以n=k+1时,等式仍然成立,故对于任意nÎN*,都有Sn=![]() ;……………8分
;……………8分
(2)因为3a5=8a12>0,所以3a5=8(a5+7d),a5= –![]() >0,所以d<0
>0,所以d<0
又a16=a5+11d = –![]() >0,a17=a5+12d =
>0,a17=a5+12d = ![]() <0,………………………………………11分
<0,………………………………………11分
所以a1>a2>a3>…>a16>0>a17>a18…,b1>b2>b3>…>b14>0>b17>b18…,
因为b15=a15a16a17<0,b16=a16a17 a18>0,………………………………………………13分
a15=a5+10d = –![]() >0,a18=a5+13d =
>0,a18=a5+13d = ![]() <0,
<0,
所以a15<–a18,所以b15> –b16,b15+b16>0,……………………………………………15分
故S16>S14,所以Sn中S16最大.………………………………………………………16分


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源:2014届江苏省无锡市高一下期中数学(艺术)试卷(解析版) 题型:解答题
(本题16分)
已知公差不为0的等差数列{ }的前4项的和为20,且
}的前4项的和为20,且 成等比数列;
成等比数列;
(1)求数列{ }通项公式;(2)设
}通项公式;(2)设 ,求数列{
,求数列{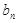 }的前n项的和
}的前n项的和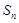 ;
;
(3)在第(2)问的基础上,是否存在
 使得
使得 成立?若存在,求出所有解;若不存在,请说明理由.
成立?若存在,求出所有解;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市崇明县高三第一学期期末考试数学 题型:解答题
(本题16分,第(1)小题3分;第(2)小题5分;第(3)小题8分)
已知数列 和
和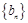 的通项分别为
的通项分别为 ,
,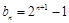 (
( ),集合
),集合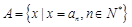 ,[来源:Zxxk.Com]
,[来源:Zxxk.Com]
 ,设
,设 . 将集合
. 将集合 中元素从小到大依次排列,构成数列
中元素从小到大依次排列,构成数列 .
.
(1)写出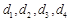 ;
;
(2)求数列 的前
的前 项的和;
项的和;
(3)是否存在这样的无穷等差数列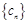 :使得
:使得 (
( )?若存在,请写出一个这样的
)?若存在,请写出一个这样的
数列,并加以证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2010年江苏省高一第二学期期末考试数学试卷 题型:解答题
(本题16分)已知{an}是等差数列,且a1=2,a1+a2+a3=12.
(1)求数列{an}的通项公式;
(2)令bn= an3n,求{bn}的前n项的和Tn.
查看答案和解析>>
科目:高中数学 来源:2010-2011年江苏省盐城市高二下学期期中考试理科数学 题型:解答题
(本题满分16分)
数列{an}中,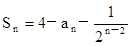 .
.
(1)求a1,a2,a3,a4;
(2)猜想an的表达式,并用数学归纳法加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com