
已知集合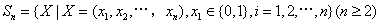 对于
对于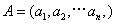 ,
,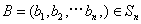 ,定义A与B的差为
,定义A与B的差为
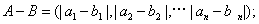
A与B之间的距离为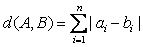
(Ⅰ)证明: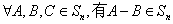 ,且
,且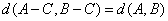 ;
;
(Ⅱ)证明: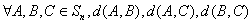 三个数中至少有一个是偶数
三个数中至少有一个是偶数
(Ⅲ) 设P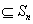 ,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为
,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为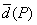 .
.
证明: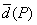 ≤
≤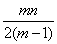 .
.
【分析】:这道题目的难点主要出现在读题上,这里简要分析一下。
题目所给的条件其实包含两个定义,第一个是关于 的,其实
的,其实 中的元素就是一个n维的坐标,其中每个坐标值都是0或者1,
也可以这样理解,就是一个n位数字的数组,每个数字都只能是0和1, 第二个定义叫距离,距离定义在两者之间,如果直观理解就是看两个数组有多少位不同,因为只有0和1才能产生一个单位的距离,因此这个大题最核心的就是处理数组上的每一位数,然后将处理的结果综合起来,就能看到整体的性质了。
中的元素就是一个n维的坐标,其中每个坐标值都是0或者1,
也可以这样理解,就是一个n位数字的数组,每个数字都只能是0和1, 第二个定义叫距离,距离定义在两者之间,如果直观理解就是看两个数组有多少位不同,因为只有0和1才能产生一个单位的距离,因此这个大题最核心的就是处理数组上的每一位数,然后将处理的结果综合起来,就能看到整体的性质了。
第一问,因为每个数位上都是0或者1,取差的绝对值仍然是0或者1,符合 的要求。然后是减去C的数位,不管减去的是0还是1,
每一个a和每一个b都是同时减去的,因此不影响他们原先的差。
的要求。然后是减去C的数位,不管减去的是0还是1,
每一个a和每一个b都是同时减去的,因此不影响他们原先的差。
第二问,先比较A和B有几个不同(因为距离就是不同的有几个),然后比较A和C有几个不同,这两者重复的(就是某一位上A和B不同,A和C不同,那么这一位上B和C就相同)去掉两次(因为在前两次比较中各计算了一次),剩下的就是B和C的不同数目,很容易得到这样的关系式: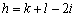 ,从而三者不可能同为奇数。
,从而三者不可能同为奇数。
第三问,首先理解P中会出现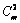 个距离,所以平均距离就是距离总和再除以
个距离,所以平均距离就是距离总和再除以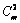 ,而距离的总和仍然可以分解到每个数位上,第一位一共产生了多少个不同,第二位一共产生了多少个不同,如此下去,直到第n位。然后思考,第一位一共m个数,只有0和1会产生一个单位距离,因此只要分开0和1的数目即可,等算出来
,而距离的总和仍然可以分解到每个数位上,第一位一共产生了多少个不同,第二位一共产生了多少个不同,如此下去,直到第n位。然后思考,第一位一共m个数,只有0和1会产生一个单位距离,因此只要分开0和1的数目即可,等算出来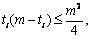 一切就水到渠成了。
一切就水到渠成了。
此外,这个问题需要注意一下数学语言的书写规范。
解:(1)设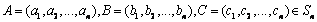
因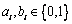 ,故
,故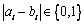 ,
,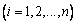
即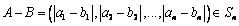
又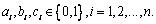
当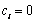 时,有
时,有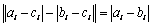 ;
;
当 时,有
时,有
故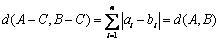
(2)设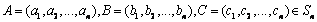
记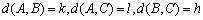
记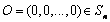 ,由第一问可知:
,由第一问可知:
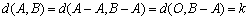
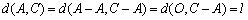

即 中1的个数为k,
中1的个数为k,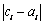 中1的个数为l,
中1的个数为l,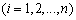
设t是使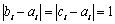 成立的i的个数,则有
成立的i的个数,则有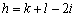 ,
,
由此可知,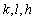 不可能全为奇数,即
不可能全为奇数,即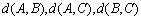 三个数中至少有一个是偶数。
三个数中至少有一个是偶数。
(3)显然P中会产生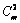 个距离,也就是说
个距离,也就是说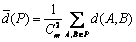 ,其中
,其中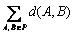 表示P中每两个元素距离的总和。
表示P中每两个元素距离的总和。
分别考察第i个位置,不妨设P中第i个位置一共出现了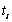 个1, 那么自然有
个1, 那么自然有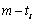 个0,因此在这个位置上所产生的距离总和为
个0,因此在这个位置上所产生的距离总和为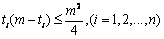 ,
,
那么n个位置的总和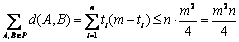
即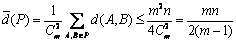
下面就一些具体问题来阐述一下解题思路,希望可以指点今后高三学生的一些复习方向。
选择题,第5题,考察知识点:极坐标系,在这个问题的设置上,命题人很巧妙地加入了一个乘积为0的现象,这违背了不少考生在之前的模拟考试中对于极坐标题的认识,认为就是简简单单的坐标转化,这一设置虽未增加多少难度,但构思仍然值得称赞。
选择题,第6题,考察知识点:常用逻辑,向量。借助函数的背景,把几个小知识点灵活地放在一起,若略有粗心便可能失分。
选择题,第7题,考察知识点:线性规划,指数函数。同样是求参数范围,这道题却能突破常规,最大值是3容易想,所有的a大于1却需要学生敏锐的观察力。
选择题,第8题,考察知识点:立体几何。四个运动的点会让考生感觉不太舒服,而几何的美妙之处很大程度上就在于如何从运动中寻找不变,这也是一向北京市命题风格,09年的选择题最后一题也体现了这个风格。
填空题,第14题,一个正方形的滚动虽然是新背景,但也不是第一次在考试中见到,但是这样的滚动方式还是会让不少学生感觉陌生,如何迅速地考察运动状态的每一次变化,就成为了解决这个问题的关键。
解答题整体难度梯度较好,第15题直接考察三角函数虽然有些出人意外,但题目本身中规中矩,跟平时三角函数的练习并没有太大区别,立体几何,概率,导数三道大题也依然维持常态,与我们平时在课堂上讲解的东西保持一致。值得说的是最后两道大题。
19题为解析几何大题,第二问很多考生反映说计算量很大,的确,如果按照一般的计算交点然后计算距离的方式去求三角形面积,计算量的确不小,但是这样做的同学大多数都是拿到题目,未详细思考直接动笔运算,事实上,如果认真考察两个三角形之间的关系,便可以发现这道题目并不需要过于复杂的运算,我后面给出的解法口算即可完成。
最后一题的立意继承了07年的压轴题立意,在离散情况下处理集合的新背景规则,带有一些组合技巧。考生的瓶颈在于读题上,大多数同学读到复杂的符号和定义的时候便头晕眼花,这说明了许多考生对于数学语言的理解层面尚浅,不能将抽象的符号语言转化为直观的认识,北京近年来的压轴题风格多为此类,下一届的高三应该在这方面多下功夫。


科目:高中数学 来源:2010年高考试题分项版文科数学之专题十五 推理与证明 题型:解答题
(本小题共13分)
已知集合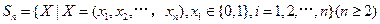 对于
对于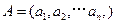 ,
,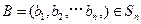 ,定义A与B的差为
,定义A与B的差为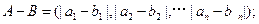
A与B之间的距离为
(Ⅰ)当n=5时,设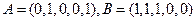 ,求
,求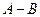 ,
,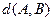 ;
;
(Ⅱ)证明: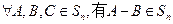 ,且
,且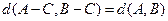 ;
;
(Ⅲ) 证明: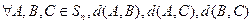 三个数中至少有一个是偶数
三个数中至少有一个是偶数
查看答案和解析>>
科目:高中数学 来源:2010年高考试题分项版理科数学之专题一 集合与简易逻辑 题型:解答题
(本小题共13分)
已知集合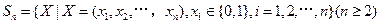 对于
对于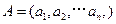 ,
,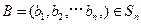 ,定义A与B的差为
,定义A与B的差为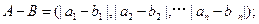
A与B之间的距离为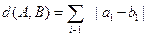
(Ⅰ)证明: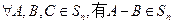 ,且
,且 ;
;
(Ⅱ)证明: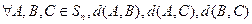 三个数中至少有一个是偶数
三个数中至少有一个是偶数
(Ⅲ) 设P ,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为
,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为 (P).
(P). 证明:
证明: (P)≤
(P)≤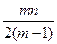 .
.
(考生务必将答案答在答题卡上,在试卷上作答无效)
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题共13分)
已知集合![]() 对于
对于![]() ,
,![]() ,定义A与B的差为
,定义A与B的差为
![]()
A与B之间的距离为![]()
(Ⅰ)证明:![]() ,且
,且![]() ;
;
(Ⅱ)证明:![]() 三个数中至少有一个是偶数
三个数中至少有一个是偶数
(Ⅲ) 设P![]() ,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为
,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为![]() .
.
证明:![]() ≤
≤![]() .
.
查看答案和解析>>
科目:高中数学 来源:2010年高考试题(北京卷)解析版(理) 题型:解答题
已知集合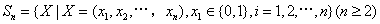 对于
对于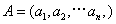 ,
,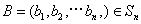 ,定义A与B的差为
,定义A与B的差为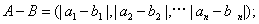 A与B之间的距离为
A与B之间的距离为
(Ⅰ)证明: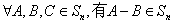 ,且
,且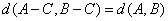 ;
;
(Ⅱ)证明: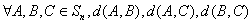 三个数中至少有一个是偶数
三个数中至少有一个是偶数
(Ⅲ) 设P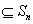 ,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为
,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为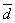 (P).
(P).
证明: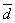 (P)≤
(P)≤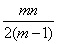 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com