
【题目】某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共100个,生产一个卫兵需5分钟,生产一个骑兵需7分钟,生产一个伞兵需4分钟,已知总生产时间不超过10小时.若生产一个卫兵可获利润5元,生产一个骑兵可获利润6元,生产一个伞兵可获利润3元.
(1)用每天生产的卫兵个数x与骑兵个数y表示每天的利润W(元);
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
【答案】
(1)解:依题意每天生产的伞兵个数为100﹣x﹣y,
所以利润W=5x+6y+3(100﹣x﹣y)
=2x+3y+300(x,y∈N).
(2)解:约束条件为

整理得 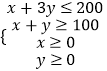
目标函数为W=2x+3y+300,
如图所示,作出可行域.
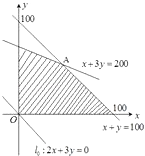
初始直线l0:2x+3y=0,平移初始直线经过点A时,W有最大值.
由 ![]() 得
得 ![]() 最优解为A(50,50),
最优解为A(50,50),
所以Wmax=550(元).
【解析】(1)依题意,每天生产的伞兵的个数为100﹣x﹣y,根据题意即可得出每天的利润;(2)先根据题意列出约束条件,再根据约束条件画出可行域,设W=2x+3y+300,再利用T的几何意义求最值,只需求出直线0=2x+3y过可行域内的点A时,从而得到W值即可.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.数据4、6、6、7、9、4的众数是4
B.一组数据的标准差是这组数据的方差的平方
C.数据3,5,7,9的标准差是数据6、10、14、18的标准差的一半
D.频率分布直方图中各小长方形的面积等于相应各组的频数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,三个内角A、B、C所对的边分别为a、b、c,且2bcosC=2a﹣c.
(1)求角B;
(2)若△ABC的面积S= ![]() ,a+c=4,求b的值.
,a+c=4,求b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了估计某水池中鱼的尾数,先从水池中捕出2000尾鱼,并给每尾鱼做上标记(不影响存活),然后放回水池,经过适当的时间,再从水池中捕出500尾鱼,其中有标记的鱼为40尾,根据上述数据估计该水池中鱼的尾数为( )
A.10000
B.20000
C.25000
D.30000
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , a1=10,an+1=9Sn+10.
(1)求证:{lgan}是等差数列;
(2)设 ![]() 对所有的n∈N*都成立的最大正整数m的值.
对所有的n∈N*都成立的最大正整数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com