练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】对于三次函数，定义是的导函数的导函数，经过讨论发现命题：“一定存在实数，使得成立”为真，请你根据这一结论判断下列命题：

    ①一定存在实数，使得成立；②一定存在实数，使得成立；③若，则；④若存在实数，且满足：，则函数在上一定单调递增，所有正确的序号是（ ）

    A. ①② B. ①③ C. ②③ D. ②④

    【答案】C

    【解析】

    根据函数f（x）的解析式求出f′（x）和f″（x），令f″（x）=0，可判断①，②，由三次函数的对称中心判断③；利用导数判断函数单调性判断④；

    ，，因为，所以②正确，但①不一定正确.由已知命题得，函数关于点中心对称，所以③正确.若存在实数，且满足：，则函数在上可以单调递增，也可以单调递减，所以④不正确.

    故选C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】我国是世界上严重缺水的国家，某市为了制定合理的节水方案，对居民用水情况进行调查，通过抽样，获得某年100为居民每人的月均用水量（单位：吨），将数据按照分成9组，制成了如图所示的频率分布直方图.

    （1）求直方图的的值；

    （2）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，说明理由.

    （3）估计居民月用水量的中位数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某厂生产产品的年固定成本为250万元，每生产千件需另投人成本万元.当年产量不足80千件时，（万元）；当年产量不小于80千件时，万元，每千件产品的售价为50万元，该厂生产的产品能全部售完.

    （1）写出年利润万元关于千件的函数关系式；

    （2）当年产量为多少千件时该厂当年的利润最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知关于的一元二次方程

    （1）若，是一枚骰子掷两次所得到的点数，求方程有两正根的概率．

    （2）若，，求方程没有实根的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在几何体P﹣ABCD中，平面ABCD⊥平面PAB ，四边形ABCD为矩形，△PAB为正三角形，若AB＝2，AD＝1，E，F 分别为AC，BP中点．

    （1）求证：EF∥平面PCD；

    （2）求直线DP与平面ABCD所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学为研究学生的身体素质与体育锻炼时间的关系，对该校300名高三学生平均每天体育锻炼时间进行调查，如表：（平均每天锻炼的时间单位：分钟）.

    平均每天锻炼的时间/分钟

    总人数

    34

    51

    59

    66

    65

    25

    将学生日均体育锻炼时间在的学生评价为“锻炼达标”.

    （1）请根据上述表格中的统计数据填写下面的列联表；

    锻炼不达标

    锻炼达标

    合计

    男

    女

    120

    40/p>

    合计

    （2）通过计算判断，是否能在犯错误的概率不超过0.05的前提下认为“锻炼达标”与性别有关？

    参考公式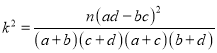：，其中.

    临界值表

    P（）

    0.10

    0.05

    0.025

    0.010

    2.706

    3.841

    5.024

    6.635

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（1）任意向轴上这一区间内投掷一个点，则该点落在区间内的概率是多少？

    （2）已知向量，，若，分别表示一枚质地均匀的正方体骰子（六个面的点数分别为1，2，3，4，5，6）先后抛掷两次时第一次、第二次出现的点数，求满足的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱中，，,分别是,的中点．

    （1）求证：∥平面；

    （2）求证：平面平面．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设均为大于1的整数.证明：存在个不被整除的整数，若将它们任意分成两组，则总有一组有若干个数的和被整除.

    查看答案和解析>>

    同步练习册答案