
【题目】已知四棱锥![]() ,底面
,底面![]() 为正方形,且
为正方形,且![]() 底面
底面![]() ,过
,过![]() 的平面与侧面
的平面与侧面![]() 的交线为
的交线为![]() ,且满足
,且满足![]() (
(![]() 表示
表示![]() 的面积).
的面积).
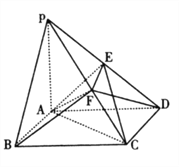
(1)证明: ![]() 平面
平面![]() ;
;
(2)当![]() 时,求点
时,求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)见解析(2) ![]()
【解析】试题分析:(1)利用平几知识由S△PEF:S四边形CDEF=1:3知E为PC的中点,连接BD交AC与G,则G为BD中点,由三角形中位线性质得EG//PB,再根据线面平行判定定理得结果(2)先根据中点得![]() ,再根据等体积法得
,再根据等体积法得![]() ,根据CD⊥平面PAD,得高CD,利用锥体体积公式得
,根据CD⊥平面PAD,得高CD,利用锥体体积公式得![]() ,即得
,即得![]() ,最后根据高等于点
,最后根据高等于点![]() 到平面
到平面![]() 的距离
的距离
试题解析:(Ⅰ)证明:由题知四边形ABCD为正方形
∴AB//CD,又![]() 平面PCD,AB
平面PCD,AB![]() 平面PCD
平面PCD
∴AB//平面PCD
又AB![]() 平面ABFE,平面ABFE∩平面PCD=EF
平面ABFE,平面ABFE∩平面PCD=EF
∴EF // AB,又AB//CD
∴EF //CD,
由S△PEF:S四边形CDEF=1:3知E、F分别为PC、PD的中点
连接BD交AC与G,则G为BD中点,
在△PBD中FG为中位线,∴ EG//PB
∵ EG//PB,EG![]() 平面ACE,PB
平面ACE,PB![]() 平面ACE
平面ACE
∴PB//平面ACE.
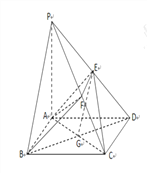
(Ⅱ)∵PA=2,AD=AB=1, ∴![]() ,
, ![]()
∵CD⊥AD,CD⊥PA,AD∩PA=A,
∴CD⊥平面PAD,∴CD⊥PD
在Rt△CDE中, ![]()
在△ACE中由余弦定理知![]()
∴![]() ,∴S△ACE=
,∴S△ACE=![]()
设点F到平面ACE的距离为![]() ,则
,则![]()
由DG⊥AC,DG⊥PA,AC∩PA=A,得DG⊥平面PAC,且![]()
∵E为PD中点,∴E到平面ACF的距离为![]()
又F为PC中点,∴S△ACF ![]() S△ACP
S△ACP ![]() ,∴
,∴![]()
由![]() 知
知![]()
∴点F到平面ACE的距离为![]() .
.


科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,且当x<0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象如图所示,

(1)画出函数f(x),x∈R剩余部分的图象,并根据图象写出函数f(x),x∈R的单调区间;(只写答案)
(2)求函数f(x),x∈R的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中,顶点A(3,7),边AB上的中线CD所在直线的方程是![]() ,边AC上的高BE所在直线的方程是
,边AC上的高BE所在直线的方程是![]() .
.
(1)求点A关于直线CD的对称点的坐标;
(2)求顶点B、C的坐标;
(3)过A作直线![]() ,使B,C两点到
,使B,C两点到![]() 的距离相等,求直线
的距离相等,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数F(x)=min{2|x1|,x22ax+4a2},
,函数F(x)=min{2|x1|,x22ax+4a2},
其中min{p,q}=![]()
(Ⅰ)求使得等式F(x)=x22ax+4a2成立的x的取值范围;
(Ⅱ)(ⅰ)求F(x)的最小值m(a);
(ⅱ)求F(x)在区间[0,6]上的最大值M(a).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小张经营某一消费品专卖店,已知该消费品的进价为每件40元,该店每月销售量(百件)与销售单价x(元/件)之间的关系用下图的一折线表示,职工每人每月工资为1000元,该店还应交付的其它费用为每月10000元.

(1)把y表示为x的函数;
(2)当销售价为每件50元时,该店正好收支平衡(即利润为零),求该店的职工人数;
(3)若该店只有20名职工,问销售单价定为多少元时,该专卖店可获得最大月利润?(注:利润=收入-支出)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com