
【题目】已知在四棱锥![]() 中,底面
中,底面![]() 是矩形,且
是矩形,且![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点.
的中点.
(1)证明:![]()
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ∥平面
∥平面![]() ,若存在,确定点
,若存在,确定点![]() 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
(3)若![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值
的余弦值
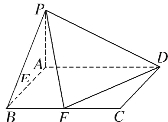
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】
试题分析:(1)利用已知的线面垂直关系建立空间直角坐标系,准确写出相关点的坐标,从而将几何证明转化为向量运算.其中灵活建系是解题的关键.(2)证明证线线垂直,只需要证明直线的方向向量垂直;(3)把向量夹角的余弦值转化为两平面法向量夹角的余弦值;(4)空间向量将空间位置关系转化为向量运算,应用的核心是要充分认识形体特征,建立恰当的坐标系,实施几何问题代数化.同时注意两点:一是正确写出点、向量的坐标,准确运算;二是空间位置关系中判定定理与性质定理条件要完备.
试题解析:解法一:(1)∵ ![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,建立如图所示的空间直角坐标系
,建立如图所示的空间直角坐标系![]() ,则
,则![]() . 2分
. 2分
不妨令![]() ∵
∵![]() ,
,![]() ∴
∴![]() ,
,
即![]() . 4分
. 4分


(2)设平面![]() 的法向量为
的法向量为![]() ,由
,由 ,得
,得![]() ,令
,令![]() ,
,
得:![]() .∴
.∴![]() . 6分
. 6分
设![]() 点坐标为
点坐标为![]()
![]() ,
,![]() ,则
,则![]() ,要使
,要使![]() ∥平面
∥平面![]() ,只需
,只需![]() ,即
,即![]() ,得
,得![]() ,从而满足
,从而满足![]() 的点
的点![]() 即为所求. 8分
即为所求. 8分
(3)∵![]() ,∴
,∴![]() 是平面
是平面![]() 的法向量,易得
的法向量,易得![]() , 9分
, 9分
又∵![]() 平面
平面![]() ,∴
,∴![]() 是
是![]() 与平面
与平面![]() 所成的角,
所成的角,
得![]() ,
,![]() ,平面
,平面![]() 的法向量为
的法向量为![]() 10分
10分
∴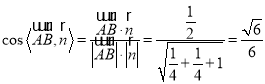 ,
,
故所求二面角![]() 的余弦值为
的余弦值为![]() . 12分
. 12分
解法二:(1)证明:连接![]() ,则
,则![]() ,
,![]() ,
,
又![]() ,∴
,∴ ![]() ,∴
,∴ ![]() 2分
2分
又![]() ,∴
,∴ ![]() ,又
,又![]() ,
,
∴ ![]() 4分
4分
(2)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,则
,则![]() ∥平面
∥平面![]() ,且有
,且有![]() 5分
5分
再过点![]() 作
作![]() ∥
∥![]() 交
交![]() 于点
于点![]() ,则
,则![]() ∥平面
∥平面![]() 且
且![]() ,∴ 平面
,∴ 平面![]() ∥平面
∥平面![]() 7分 ∴
7分 ∴ ![]() ∥平面
∥平面![]() .从而满足
.从而满足![]() 的点
的点![]() 即为所求. 8分
即为所求. 8分
(3)∵![]() 平面
平面![]() ,∴
,∴![]() 是
是![]() 与平面
与平面![]() 所成的角,且
所成的角,且![]() .
.
∴ ![]() 9分
9分
取![]() 的中点
的中点![]() ,则
,则![]()
![]()
![]() ,
,![]()
![]() 平面
平面![]() ,
,
在平面![]() 中,过
中,过![]() 作
作![]() ,连接
,连接![]() ,则
,则![]() ,
,
则![]() 即为二面角
即为二面角![]() 的平面角 10分
的平面角 10分
∵![]() ∽
∽![]() ,∴
,∴ ![]() ,∵
,∵![]() ,且
,且![]()
∴ ![]() ,
,![]() ,∴
,∴ ![]() 12分
12分


科目:高中数学 来源: 题型:
【题目】为了普及环保知识,增强环保意识,某校从理科甲班抽取60人,从文科乙班抽取50人参加环保知识测试.
优秀人数 | 非优秀人数 | 总计 | |
甲班 | |||
乙班 | 30 | ||
总计 | 60 |
(Ⅰ)根据题目完成![]() 列联表,并据此判断是否有
列联表,并据此判断是否有![]() 的把握认为环保知识成绩优秀与学生的文理分类有关.
的把握认为环保知识成绩优秀与学生的文理分类有关.
(Ⅱ)现已知![]() ,
, ![]() ,
, ![]() 三人获得优秀的概率分别为
三人获得优秀的概率分别为![]() ,
, ![]() ,
, ![]() ,设随机变量
,设随机变量![]() 表示
表示![]() ,
, ![]() ,
, ![]() 三人中获得优秀的人数,求
三人中获得优秀的人数,求![]() 的分布列及期望
的分布列及期望![]() .
.
附:  ,
, ![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)若直线![]() 是函数
是函数![]() 图象的一条切线,求实数
图象的一条切线,求实数![]() 的值;
的值;
(2)若函数![]() 在
在![]() 上的最大值为
上的最大值为![]() (
(![]() 为自然对数的底数),求实数
为自然对数的底数),求实数![]() 的值;
的值;
(3)若关于![]() 的方程
的方程![]() 有且仅有唯一的实数根,求实数
有且仅有唯一的实数根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列几个命题
①奇函数的图象一定通过原点
②函数y= ![]() 是偶函数,但不是奇函数
是偶函数,但不是奇函数
③函数f(x)=ax﹣1+3的图象一定过定点P,则P点的坐标是(1,4)
④若f(x+1)为偶函数,则有f(x+1)=f(﹣x﹣1)
⑤若函数f(x)= 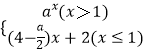 在R上的增函数,则实数a的取值范围为[4,8)
在R上的增函数,则实数a的取值范围为[4,8)
其中正确的命题序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中, ![]() ,
, ![]() 为边
为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻转成
翻转成![]() .若
.若![]() 为线段
为线段![]() 的中点,则在
的中点,则在![]() 翻折过程中:
翻折过程中:
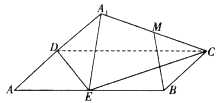
①![]() 是定值;②点
是定值;②点![]() 在某个球面上运动;
在某个球面上运动;
③存在某个位置,使![]() ;④存在某个位置,使
;④存在某个位置,使![]() 平面
平面![]() .
.
其中正确的命题是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研小组研究发现:一棵水果树的产量![]() (单位:百千克)与肥料费用(单位:百元)满足如下关系:
(单位:百千克)与肥料费用(单位:百元)满足如下关系:  .此外,还需要投入其它成本(如施肥的人工费等)
.此外,还需要投入其它成本(如施肥的人工费等)![]() 百元.已知这种水果的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水果树获得的利润为
百元.已知这种水果的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水果树获得的利润为![]() (单位:百元).
(单位:百元).
(1)求![]() 的函数关系式;
的函数关系式;
当投入的肥料费用为多少时,该水果树获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点 P 与定点![]() 的距离和它到定直线 x 4 的距离的比是1: 2 ,记动点 P 的轨迹为曲线 E.
的距离和它到定直线 x 4 的距离的比是1: 2 ,记动点 P 的轨迹为曲线 E.
(1)求曲线 E 的方程;
(2)设 A 是曲线 E 上的一个点,直线 AF 交曲线 E 于另一点 B,以 AB 为边作一个平行四边形,顶点 A、B、C、D 都在轨迹 E 上,判断平行四边形 ABCD 能否为菱形,并说明理由;
(3)当平行四边形 ABCD 的面积取到最大值时,判断它的形状,并求出其最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com