
分析 (1)根据递推式,依次令n=2,3,4计算a2,a3,a4;
(2)根据前4相猜想通项公式,验证n=1时猜想成立,假设n=k时猜想成立,根据条件推导ak+1得出结论.
解答 解:(1)a1=$\frac{1}{3}$,a2=$\frac{1}{15}$,a3=$\frac{1}{35}$,a4=$\frac{1}{63}$.
(2)猜想:an=$\frac{1}{(2n-1)(2n+1)}$.
证明:①当n=1时,猜想显然成立.
②假设n=k时猜想成立,即ak=$\frac{1}{(2k-1)(2k+1)}$.
∵$\frac{{a}_{1}+{a}_{2}+…+{a}_{n}}{2n-1}$=nan,∴$\frac{{a}_{1}+{a}_{2}+…+{a}_{n}}{n}$=(2n-1)an.
∴$\frac{{a}_{1}+{a}_{2}+…+{a}_{k}+{a}_{k+1}}{k+1}=(2k+1){a}_{k+1}$,
∴a1+a2+…+ak=(2k2+3k)ak+1,
又a1+a2+…+ak=(2k2-k)ak=$\frac{k}{2k+1}$,
∴ak+1=$\frac{{a}_{1}+{a}_{2}+…+{a}_{k}}{2{k}^{2}+3k}$=$\frac{1}{(2k+1)(2k+3)}$,
∴当n=k+1时,猜想成立.
由①②可知,对一切n∈N+,都有an=$\frac{1}{(2n-1)(2n+1)}$.
点评 本题考查了数列的通项公式,数学归纳法的证明,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
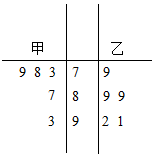 甲、乙两位同学在高一年级的5次考试中,数学成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别是$\overline{x_1},\overline{x_2}$,则下列叙述正确的是( )
甲、乙两位同学在高一年级的5次考试中,数学成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别是$\overline{x_1},\overline{x_2}$,则下列叙述正确的是( )| A. | $\overline{x_1}$>$\overline{x_2}$,乙比甲成绩稳定 | B. | $\overline{x_1}$>$\overline{x_2}$,甲比乙成绩稳定 | ||
| C. | $\overline{x_1}$<$\overline{x_2}$,乙比甲成绩稳定 | D. | $\overline{x_1}$<$\overline{x_2}$,甲比乙成绩稳定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | $\sqrt{6}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{2}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年内蒙古高二理上月考一数学理试卷(解析版) 题型:选择题
已知a,b,c∈R,命题“若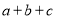 =3,则
=3,则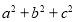 ≥3”的否命题是( )
≥3”的否命题是( )
A.若a+b+c≠3,则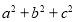 <3
<3
B.若a+b+c=3,则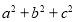 <3
<3
C.若a+b+c≠3,则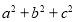 ≥3
≥3
D.若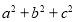 ≥3,则a+b+c=3
≥3,则a+b+c=3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com