
【题目】某种产品的质量以其质量指标衡量,并依据质量指标值划分等级如表:
质量指标值m | m<185 | 185≤m<205 | M≥205 |
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
(1)根据以上抽样调查的数据,能否认为该企业生产这种产品符合“一、二等品至少要占到全部产品的92%的规定”?
(2)在样本中,按产品等级用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品的质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值X近似满足X~N(218,140),则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
【答案】
(1)解:根据抽样调查数据,一、二等品所占比例的估计值为
0.200+0.300+0.260+0.090+0.025=0.875,
由于该估计值小于0.92,故不能认为该企业生产的这种产品
符合“一、二等品至少要占到全部产品的92%的规定”;
(2)由频率分布直方图知,一、二、三等品的频率分别为0.375、0.5和0.125,
故在样本中,一等品3件,二等品4件,三等品1件;
再从这8件产品中随机抽取4件,一、二、三等品都有的情形有2种,
①一等品2件,二等品1件,三等品1件;
②一等品1件,二等品2件,三等品1件,
故所求的概率为P= ![]() =
= ![]() ;
;
(3)“质量提升月”活动前,该企业这种产品的质量指标值的均值约为
170×0.025+180×0.1+190×0.2+200×0.3+210×0.26+220×0.09+230×0.025=200.4;
“质量提升月”活动后,产品质量指标值X近似满足X~N(218,140),
则数学期望E(X)=218;
所以“质量提升月”活动后的质量指标值的均值比活动前大约提升了
218﹣200.4=17.6.
【解析】(1)根据抽样调查数据计算一、二等品所占比例的估计值,判断该企业生产的这种产品是否符合“一、二等品至少要占到全部产品的92%的规定”;(2)由频率分布直方图知一、二、三等品的频率值,计算样本中一等品、二等品、三等品的件数,求出从这8件产品中随机抽取4件,一、二、三等品都有的情形,计算所求的概率值;(3)计算“质量提升月”活动前、后产品质量指标值的均值,比较得出结论.
【考点精析】本题主要考查了频率分布直方图的相关知识点,需要掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图所示,三棱柱ABC﹣A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=60°.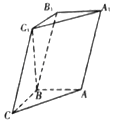
(Ⅰ)求证:C1B⊥平面ABC;
(Ⅱ)E是棱CC1所在直线上的一点,若二面角A﹣B1E﹣B的正弦值为 ![]() ,求CE的长.
,求CE的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3 ![]() (1﹣a)x2﹣3ax+1,a>0.
(1﹣a)x2﹣3ax+1,a>0.
(1)试讨论f(x)(x≥0)的单调性;
(2)证明:对于正数a,存在正数p,使得当x∈[0,p]时,有﹣1≤f(x)≤1;
(3)设(1)中的p的最大值为g(a),求g(a)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项a1=m,其前n项和为Sn , 且满足Sn+Sn+1=3n2+2n,若对n∈N+ , an<an+1恒成立,则m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点P是双曲线 ![]() 的右支上一点,其左,右焦点分别为F1 , F2 , 直线PF1与以原点O为圆心,a为半径的圆相切于A点,线段PF1的垂直平分线恰好过点F2 , 则离心率的值为( )
的右支上一点,其左,右焦点分别为F1 , F2 , 直线PF1与以原点O为圆心,a为半径的圆相切于A点,线段PF1的垂直平分线恰好过点F2 , 则离心率的值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数h(x)=﹣|x﹣3|.
(1)若h(x)﹣|x﹣2|≤n对任意的x>0恒成立,求实数n的最小值;
(2)若函数f(x)= 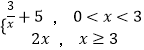 ,求函数g(x)=f(x)+h(x)的值域.
,求函数g(x)=f(x)+h(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣a+lnx.
(Ⅰ)若a=1,求证:当x>1时,f(x)>2x﹣1;
(Ⅱ)若存在x0≥e,使f(x0)<2lnx0 , 求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的多面体ABCDEF中,ABCD为直角梯形,AB∥CD,∠DAB=90°,四边形ADEF为等腰梯形,EF∥AD,已知AE⊥EC,AB=AF=EF=2,AD=CD=4.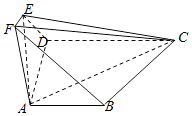
(1)求证:平面ABCD⊥平面ADEF;
(2)求直线CF与平面EAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() x3+x2﹣3x,若方程|f(x)|2+t|f(x)|+1=0有12个不同的根,则实数t的取值范围为( )
x3+x2﹣3x,若方程|f(x)|2+t|f(x)|+1=0有12个不同的根,则实数t的取值范围为( )
A.(﹣ ![]() ,﹣2)
,﹣2)
B.(﹣∞,﹣2)
C.﹣ ![]() <t<﹣2
<t<﹣2
D.(﹣1,2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com