
【题目】设F是椭圆C:![]() (a>b>0)的一个焦点,P是椭圆C上的点,圆x2+y2=
(a>b>0)的一个焦点,P是椭圆C上的点,圆x2+y2=![]() 与线段PF交于A,B两点,若A,B三等分线段PF,则椭圆C的离心率为( )
与线段PF交于A,B两点,若A,B三等分线段PF,则椭圆C的离心率为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】D
【解析】
取线段PF的中点H,连接OH,OA,由题意可得OH⊥AB,设|OH|=d,根据椭圆的定义以及在Rt△OHA中,可得a=5d,在Rt△OHF中,利用勾股定理即可求解.
如图,取线段PF的中点H,连接OH,OA.
设椭圆另一个焦点为E,连接PE.
∵A,B三等分线段PF,∴H也是线段AB的中点,即OH⊥AB.
设|OH|=d,则|PE|=2d,|PF|=2a-2d,|AH|=![]() .
.
在Rt△OHA中,|OA|2=|OH|2+|AH|2,解得a=5d.
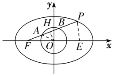
在Rt△OHF中,|FH|=![]() ,|OH|=
,|OH|=![]() ,|OF|=c.
,|OF|=c.
由|OF|2=|OH|2+|FH|2,
化简得17a2=25c2,![]() .
.
即椭圆C的离心率为![]() .
.
故选:D.


科目:高中数学 来源: 题型:
【题目】某中学有初中学生1800人,高中学生1200人. 为了解学生本学期课外阅读时间,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们课外阅读时间,然后按“初中学生”和“高中学生”分为两组,再将每组学生的阅读时间(单位:小时)分为5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并分别加以统计,得到如图所示的频率分布直方图.
,并分别加以统计,得到如图所示的频率分布直方图.
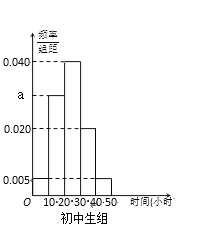
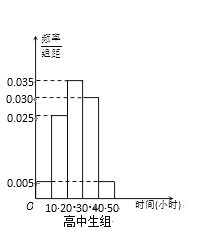
(Ⅰ)写出![]() 的值;试估计该校所有学生中,阅读时间不小于30个小时的学生人数;
的值;试估计该校所有学生中,阅读时间不小于30个小时的学生人数;
(Ⅱ)从阅读时间不足10个小时的样本学生中随机抽取2人,求至少抽到1名高中生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 的底面
的底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() .
.
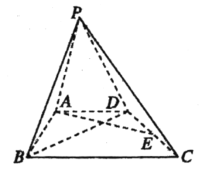
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,试问“在侧面
,试问“在侧面![]() 内是否存在一点
内是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,连接椭圆四个顶点得到的菱形的面积为4.
,连接椭圆四个顶点得到的菱形的面积为4.
(1)求椭圆的方程;
(2)设![]() 是椭圆的右顶点,过点
是椭圆的右顶点,过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
,![]() 分别与椭圆交于
分别与椭圆交于![]() ,
,![]() 两点,求证:直线
两点,求证:直线![]() 过定点;
过定点;
(3)(只理科做)过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
,![]() ,
,![]() 与圆
与圆![]() :
:![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 交椭圆于另一点
交椭圆于另一点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)当a≤0时,讨论函数f(x)的单调性;
(2)是否存在实数a,对任意的x1,x2![]() (0,+∞),且x1≠x2,都有
(0,+∞),且x1≠x2,都有![]() 恒成立.若存在,求出a的取值范围;若不存在,说明理由.
恒成立.若存在,求出a的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将![]() 个编号为
个编号为![]() 、
、![]() 、
、![]() 、
、![]() 的不同小球全部放入
的不同小球全部放入![]() 个编号为
个编号为![]() 、
、![]() 、
、![]() 、
、![]() 的
的![]() 个不同盒子中.求:
个不同盒子中.求:
(1)每个盒至少一个球,有多少种不同的放法?
(2)恰好有一个空盒,有多少种不同的放法?
(3)每盒放一个球,并且恰好有一个球的编号与盒子的编号相同,有多少种不同的放法?
(4)把已知中![]() 个不同的小球换成四个完全相同的小球(无编号),其余条件不变,恰有一个空盒,有多少种不同的放法?
个不同的小球换成四个完全相同的小球(无编号),其余条件不变,恰有一个空盒,有多少种不同的放法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两台机床生产同一型号零件,记生产的零件的尺寸为![]() ,相关行业质检部门规定:若
,相关行业质检部门规定:若![]() ,则该零件为优等品;若
,则该零件为优等品;若![]() ,则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质里检测得到下表数据:
,则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质里检测得到下表数据:
尺寸 |
|
|
|
|
|
|
甲机床零件频数 | 2 | 3 | 20 | 20 | 4 | 1 |
乙机床零件频数 | 3 | 5 | 17 | 13 | 8 | 4 |
(Ⅰ)设生产每件产品的利润为:优等品3元,中等品1元,次品亏本1元.若将频率视为概率,试估算甲机床生产一件零件的利润的数学期望;
(Ⅱ)根据已知条件完成下面的列联表,并据此数据回答:是否有![]() 的把握认为“零件优等与否和所用机床有关”?
的把握认为“零件优等与否和所用机床有关”?
甲机床 | 乙机床 | 合计 | |
优等品 | |||
非优等品 | |||
合计 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com