
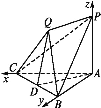
【题目】如图,在三棱锥P-ABC中,PA⊥底面ABC,△ABC是直角三角形,且PA=AB=AC.又平面QBC垂直于底面ABC.
(1)求证:PA∥平面QBC;
(2)若PQ⊥平面QBC,求锐二面角Q-PB-A的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)过点Q作QD⊥BC交BC于点D,则QD⊥平面ABC,而PA⊥平面ABC,可得QD∥PA,从而问题得证。
(2)建立空间直角坐标系,找出二面角Q-PB-A所在的两个平面的法向量,求出法向量夹角的余弦值,结合角的范围,得出最终结果。
(1)证明过点Q作QD⊥BC交BC于点D,
因为平面QBC⊥平面ABC,
所以QD⊥平面ABC.
又PA⊥平面ABC,
所以QD∥PA.
而QD平面QBC,PA平面QBC,
所以PA∥平面QBC.
(2)解因为PQ⊥平面QBC,
所以∠PQB=∠PQC=90°.
又PB=PC,PQ=PQ,
所以△PQB≌△PQC,
所以BQ=CQ.
所以点D是BC的中点,连接AD,则AD⊥BC,因此AD⊥平面QBC,故四边形PADQ是矩形.
分别以AC,AB,AP所在直线为x,y,z轴,建立如图所示的空间直角坐标系.
设PA=2a,则Q(a,a,2a),B(0,2a,0),P(0,0,2a).
设平面QPB的法向量为n=(x,y,z),
因为![]() =(a,a,0),
=(a,a,0),![]() =(0,2a,-2a),
=(0,2a,-2a),
所以![]()
取n=(1,-1,-1).
又平面PAB的一个法向量为m=![]() =(1,0,0),
=(1,0,0),
设锐二面角Q-PB-A的大小为θ,
则cos θ=|cos<m,n>|=![]() ,
,
即锐二面角Q-PB-A的余弦值等于![]() .
.


科目:高中数学 来源: 题型:
【题目】函数f(x)= ![]() .
.
(1)若a=5,求函数f(x)的定义域A;
(2)设B={x|﹣1<x<2},当实数a,b∈B∩(RA)时,求证: ![]() <|1+
<|1+ ![]() |.
|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a∈Z,已知定义在R上的函数f(x)=2x4+3x3﹣3x2﹣6x+a在区间(1,2)内有一个零点x0 , g(x)为f(x)的导函数.
(Ⅰ)求g(x)的单调区间;
(Ⅱ)设m∈[1,x0)∪(x0 , 2],函数h(x)=g(x)(m﹣x0)﹣f(m),求证:h(m)h(x0)<0;
(Ⅲ)求证:存在大于0的常数A,使得对于任意的正整数p,q,且 ![]() ∈[1,x0)∪(x0 , 2],满足|
∈[1,x0)∪(x0 , 2],满足| ![]() ﹣x0|≥
﹣x0|≥ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,∠ABC=![]() ,D是棱AC的中点,且AB=BC=BB1=2.
,D是棱AC的中点,且AB=BC=BB1=2.

(1)求证:AB1∥平面BC1D;
(2)求异面直线AB1与BC1所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}和等比数列{bn}满足a1=b1=1,a2+a4=10,b2b4=a5 .
(Ⅰ)求{an}的通项公式;
(Ⅱ)求和:b1+b3+b5+…+b2n﹣1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于概率和统计的几种说法:
①10名工人某天生产同一种零件,生产的件数分别是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则a,b,c的大小关系为c>a>b;
②样本4,2,1,0,-2的标准差是2;
③在面积为S的△ABC内任选一点P,则随机事件“△PBC的面积小于![]() ”的概率为
”的概率为![]() ;
;
④从写有0,1,2,…,9的十张卡片中,有放回地每次抽一张,连抽两次,则两张卡片上的数字各不相同的概率是![]() .
.
其中正确说法的序号有________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com