
ЎѕМвДїЎїѕЭДіЖшПуЦРРД№ЫІмєНФ¤ІвЈє·ўЙъУЪMµШµДЙііѕ±©Т»Ц±ПтХэДП·ЅПтТЖ¶ЇЈ¬ЖдТЖ¶ЇЛЩ¶Иv(km/h)УлК±јдt(h)µДєЇКэНјПуИзНјЛщКѕЈ®№эПЯ¶ОOCЙПТ»µгT(t,0)ЧчєбЦбµДґ№ПЯlЈ¬МЭРОOABCФЪЦ±ПЯlЧуІаІї·ЦµДГж»эјґК±јдt(h)ДЪЙііѕ±©Лщѕ№эµДВ·іМs(km)Ј®

(1)µ±tЈЅ4К±Ј¬ЗуsµДЦµЈ»
(2)Ѕ«sЛжt±д»ЇµД№жВЙУГКэС§№ШПµКЅ±нКѕіцАґЈ»
(3)ИфNіЗО»УЪMµШХэДП·ЅПтЈ¬ЗТѕаMµШ650 kmЈ¬КФЕР¶ПХвіЎЙііѕ±©КЗ·с»бЗЦП®µЅNіЗЈ¬Из№ы»бЈ¬ФЪЙііѕ±©·ўЙъєу¶аі¤К±јдЛьЅ«ЗЦП®µЅNіЗЈїИз№ыІ»»бЈ¬ЗлЛµГчАнУЙЈ®
Ўѕґр°ёЎїЈЁ1Ј©24Ј»ЈЁ2Ј©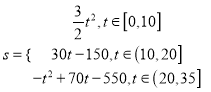 Ј»ЈЁ3Ј©Йііѕ±©·ўЙъ30 hєуЅ«ЗЦП®µЅNіЗЈ®
Ј»ЈЁ3Ј©Йііѕ±©·ўЙъ30 hєуЅ«ЗЦП®µЅNіЗЈ®
ЎѕЅвОцЎїКФМв·ЦОцЈєЈЁ1Ј©ПИЗуіцПЯ¶ОOAµДЅвОцКЅОЄv=4tЈ¬И»єу°Сt=10Ц±ЅУґъИлЗуіцґЛК±µДЛЩ¶ИЈ¬јґїЙЗуіцSЈЁtЈ©µДЦµЈ»ЈЁ2Ј©ПИ·Ц¶ОЗуіцЛЩ¶ИvУлК±јдtµДєЇКэєЇКэ№ШПµЈ¬ФЩ·Ц±ріЛТФК±јдјґїЙЗуµГ¶ФУ¦µДєЇКэSЈЁtЈ©µДЅвОцКЅЈ»ЈЁ3Ј©ПИУЙ·Ц¶ОєЇКэµДЅвОцКЅТФј°¶ФУ¦µД¶ЁТеУтїЙТФЗуµГЖдЧоґуЦµЈ¬·ўПЦЖдЧоґуЦµґуУЪ650Ј¬јґїЙПВЅбВЫ»бЗЦП®µЅNіЗЈ¬ФЩ°СSЈЁtЈ©=650ґъИлјґїЙЗуіц¶ФУ¦µДtЈ®
КФМвЅвОцЈєЅвЈєЈЁ1Ј©УЙНјПсїЙЦЄЈ¬µ±tЈЅ4К±Ј¬vЈЅ3ЎБ4ЈЅ12Ј¬
ЛщТФSЈЅ![]() ЎБ4ЎБ12ЈЅ24 kmЈ®
ЎБ4ЎБ12ЈЅ24 kmЈ®
ЈЁ2Ј©µ±0ЎЬtЎЬ10К±Ј¬SЈЅ![]() Ў¤tЎ¤3tЈЅ
Ў¤tЎ¤3tЈЅ![]() Ј»
Ј»
µ±10<tЎЬ20К±Ј¬SЈЅ![]() ЎБ10ЎБ30Ј«30ЈЁtЈ10Ј©ЈЅ30tЈ150Ј»
ЎБ10ЎБ30Ј«30ЈЁtЈ10Ј©ЈЅ30tЈ150Ј»
µ±20<tЎЬ35К±Ј¬SЈЅ![]() ЎБ10ЎБ30Ј«10ЎБ30Ј«ЈЁtЈ20Ј©ЎБ30Ј
ЎБ10ЎБ30Ј«10ЎБ30Ј«ЈЁtЈ20Ј©ЎБ30Ј![]() ЎБЈЁtЈ20Ј©ЎБ2ЈЁtЈ20Ј©ЈЅ
ЎБЈЁtЈ20Ј©ЎБ2ЈЁtЈ20Ј©ЈЅ![]() Ј®
Ј®
ЧЫЙПїЙЦЄЈ¬ 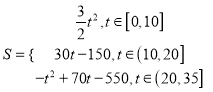 Ј®
Ј®
ЈЁ3Ј©ТтОЄµ±tЎК[0Ј¬10]К±Ј¬SmaxЈЅ![]() ЎБ102ЈЅ150<650Ј¬
ЎБ102ЈЅ150<650Ј¬
µ±tЎКЈЁ10Ј¬20]К±Ј¬SmaxЈЅ30ЎБ20Ј150ЈЅ450<650Ј¬
ЛщТФµ±tЎКЈЁ20Ј¬35]К±Ј¬Бо![]() Ј¬ЅвµГ
Ј¬ЅвµГ![]() Ј®ТтОЄ20<tЎЬ35Ј¬ЛщТФtЈЅ30Ј®
Ј®ТтОЄ20<tЎЬ35Ј¬ЛщТФtЈЅ30Ј®
№КЙііѕ±©·ўЙъ30 hєуЅ«ЗЦП®µЅNіЗЈ®



| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄ![]() КЗ¶ЁТеФЪ
КЗ¶ЁТеФЪ![]() ЙПµДєЇКэ,ЗТ¶ФИОТв
ЙПµДєЇКэ,ЗТ¶ФИОТв![]() ¶јУР
¶јУР![]() ,ЗТВъЧг
,ЗТВъЧг![]() Ј¬
Ј¬![]() ,Фт
,Фт![]() =
=
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄ![]() ОЄНЦФІ
ОЄНЦФІ![]() µДТ»ёцЅ№µгЈ¬№эФµгµДЦ±ПЯ
µДТ»ёцЅ№µгЈ¬№эФµгµДЦ±ПЯ![]() УлНЦФІЅ»УЪ
УлНЦФІЅ»УЪ![]() БЅµгЈ¬ЗТ
БЅµгЈ¬ЗТ![]() Ј¬
Ј¬ ![]() µДГж»эОЄ
µДГж»эОЄ![]() .
.
ЈЁўсЈ©ЗуНЦФІµДАлРДВКЈ»
ЈЁўтЈ©Иф![]() Ј¬№эµг
Ј¬№эµг![]() ЗТІ»УлЧш±кЦбґ№Ц±µДЦ±ПЯЅ»НЦФІУЪ
ЗТІ»УлЧш±кЦбґ№Ц±µДЦ±ПЯЅ»НЦФІУЪ![]() БЅµгЈ¬ПЯ¶О
БЅµгЈ¬ПЯ¶О![]() µДґ№Ц±ЖЅ·ЦПЯУл
µДґ№Ц±ЖЅ·ЦПЯУл![]() ЦбЅ»УЪµг
ЦбЅ»УЪµг![]() Ј¬Зуµг
Ј¬Зуµг![]() єбЧш±кµДИЎЦµ·¶О§.
єбЧш±кµДИЎЦµ·¶О§.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪЎчABCЦРЈ¬aЎўbЎўc·Ц±рОЄДЪЅЗAЎўBЎўCµД¶Ф±ЯЈ¬ЗТ2asinA=ЈЁ2b+cЈ©sinB+ЈЁ2c+bЈ©sinC
ЈЁ1Ј©ЗуAµДґуРЎЈ»
ЈЁ2Ј©ИфsinB+sinC=1Ј¬КФЕР¶ПЎчABCµДРОЧґЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэfЈЁxЈ©=ax3+cxЈЁaЈѕ0Ј©Ј¬ЖдНјПуФЪµгЈЁ1Ј¬fЈЁ1Ј©Ј©ґ¦µДЗРПЯУлЦ±ПЯ x©Ѓ6y+21=0ґ№Ц±Ј¬µјєЇКэ
fЎдЈЁxЈ©µДЧоРЎЦµОЄ©Ѓ12Ј®
ЈЁ1Ј©ЗуєЇКэfЈЁxЈ©µДЅвОцКЅЈ»
ЈЁ2Ј©Зуy=fЈЁxЈ©ФЪxЎК[©Ѓ2Ј¬2]µДЦµУтЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄНЦФІµДЦРРДФЪФµгЈ¬Ѕ№µгФЪ![]() ЦбЙПЈ¬АлРДВКОЄ
ЦбЙПЈ¬АлРДВКОЄ![]() Ј¬ИфЕЧОпПЯ
Ј¬ИфЕЧОпПЯ![]() µДЅ№µгУлНЦФІµДТ»ёцЅ№µгЦШєПЈ®
µДЅ№µгУлНЦФІµДТ»ёцЅ№µгЦШєПЈ®
ЈЁ1Ј©ЗуНЦФІµД±кЧј·ЅіМЈ»
ЈЁ2Ј©№эНЦФІµДЧуЅ№µг![]() Ј¬ЗТР±ВКОЄ
Ј¬ЗТР±ВКОЄ![]() µДЦ±ПЯ
µДЦ±ПЯ![]() Ѕ»НЦФІУЪ
Ѕ»НЦФІУЪ![]() Ј¬
Ј¬ ![]() БЅµгЈ¬Зу
БЅµгЈ¬Зу![]() µДГж»эЈ®
µДГж»эЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТ»НшХѕУЄПъІїОЄНіјЖДіКРНшУС2017Дк12ФВ12ИХФЪДіНшµкµДНш№єЗйїцЈ¬Лж»ъійІйБЛёГКР60ГыНшУСФЪёГНшµкµДНш№єЅр¶оЗйїцЈ¬Из±нЈє
Нш№єЅр¶о (µҐО»ЈєЗ§ФЄ) | ЖµКэ | ЖµВК |
| 3 |
|
|
|
|
| 9 |
|
| 15 |
|
| 18 |
|
|
|
|
єПјЖ | 60 |
|
ИфЅ«µ±ИХНш№єЅр¶оІ»РЎУЪ2З§ФЄµДНшУСіЖОЄЎ°Нш№єґпИЛЎ±Ј¬Нш№єЅр¶оРЎУЪ2З§ФЄµДНшУСіЖОЄЎ°Нш№єМЅХЯЎ±Ј¬ТСЦЄЎ°Нш№єґпИЛЎ±УлЎ°Нш№єМЅХЯЎ±ИЛКэµД±ИАэОЄ![]() .
.
ЈЁ1Ј©И·¶Ё![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() µДЦµЈ¬ІўІ№И«ЖµВК·ЦІјЦ±·ЅНјЈ»
µДЦµЈ¬ІўІ№И«ЖµВК·ЦІјЦ±·ЅНјЈ»

ЈЁ2Ј©КФёщѕЭЖµВК·ЦІјЦ±·ЅНј№АЛгХв60ГыНшУСµ±ИХФЪёГНшµкНш№єЅр¶оµДЖЅѕщКэєНЦРО»КэЈ»ИфЖЅѕщКэєНЦРО»КэЦБЙЩУРТ»ёцІ»µНУЪ2З§ФЄЈ¬ФтёГНшµкµ±ИХЖАОЄЎ°»К№ЪµкЎ±Ј¬КФЕР¶ПёГНшµкµ±ИХДЬ·с±»ЖАОЄЎ°»К№ЪµкЎ±.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЎѕСЎРЮ4©Ѓ1јёєОЦ¤ГчСЎЅІЎї
ИзНјЈ¬CDОЄЎчABCНвЅУФІµДЗРПЯЈ¬ABµДСУі¤ПЯЅ»Ц±ПЯCDУЪµгDЈ¬EЎўF·Ц±рОЄПТABУлПТACЙПµДµгЈ¬ЗТBCAE=DCAFЈ¬BЎўEЎўFЎўCЛДµг№ІФІЈ®
ЈЁ1Ј©Ц¤ГчЈєCAКЗЎчABCНвЅУФІµДЦ±ѕ¶Ј»
ЈЁ2Ј©ИфDB=BE=EAЈ¬Зу№эBЎўEЎўFЎўCЛДµгµДФІµДГж»эУлЎчABCНвЅУФІГж»эµД±ИЦµЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФД¶БИзПВіМРтїтНјЈ¬Из№ыКдіцi=5Ј¬ДЗГґФЪїХ°ЧѕШРОїтЦРУ¦МоИлµДУпѕдОЄЈЁ Ј© 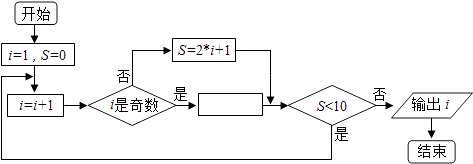
A.S=2*i©Ѓ2
B.S=2*i©Ѓ1
C.S=2*I
D.S=2*i+4
Ійїґґр°ёєНЅвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com