
【题目】已知圆C1:x2+y2=4与圆C2:(x﹣1)2+(y﹣3)2=4,过动点P(a,b)分别作圆C1、圆C2的切线PM,PN,(M,N分别为切点),若|PM|=|PN|,则a2+b2﹣6a﹣4b+13的最小值是( )
A.5
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:∵过动点P(a,b)分别作圆C1,圆C2的切线PM,PN( M、N分别为切点),若PM=PN,
∴|PC1|2=|PC2|2,
即a2+b2=(a﹣1)2+(b﹣3)2,
即a+3b﹣5=0,即动点P(a,b)在直线x+3y﹣5=0上,
a2+b2﹣6a﹣4b+13=(a﹣3)2+(b﹣2)2的几何意义为P到定点(3,2)的距离的平方,
则点(3,2)到直线x+3y﹣5=0的距离为 ![]() =
= ![]() ,
,
故a2+b2﹣6a﹣4b+13的最小值为 ![]() ,
,
故选B.
【考点精析】通过灵活运用直线与圆的三种位置关系,掌握直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点即可以解答此题.


科目:高中数学 来源: 题型:
【题目】若函数f(x)在定义域内存在实数x0 , 使得f(x0+1)=f(x0)+f(1)成立,则称函数f(x)有“飘移点”x0 . (Ⅰ)证明f(x)=x2+ex在区间 ![]() 上有“飘移点”(e为自然对数的底数);
上有“飘移点”(e为自然对数的底数);
(Ⅱ)若 ![]() 在区间(0,+∞)上有“飘移点”,求实数a的取值范围.
在区间(0,+∞)上有“飘移点”,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆方程为 ![]() =1(a>0,b>0),其右焦点为F(4,0),过点F的直线交椭圆与A,B两点.若AB的中点坐标为(1,﹣1),则椭圆的方程为( )
=1(a>0,b>0),其右焦点为F(4,0),过点F的直线交椭圆与A,B两点.若AB的中点坐标为(1,﹣1),则椭圆的方程为( )
A.![]() =1
=1
B.![]() =1
=1
C.![]() +
+ ![]() =1
=1
D.![]() =1
=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x<﹣2或x>0},B={x|( ![]() )x≥3} (Ⅰ)求A∪B
)x≥3} (Ⅰ)求A∪B
(Ⅱ)若集合C={x|a<x≤a+1},且A∩C=C,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面给出了2010年亚洲一些国家的国民平均寿命(单位:岁)
国家 平均寿命 | 国家 平均寿命 | 国家 平均寿命 | 国家 平均寿命 | 国家 平均寿命 |
阿曼 76.1 | 泰国 73.7 | 阿富汗 59.0 | 尼泊尔 68.0 | 孟加拉国 70.1 |
(1)请补齐频率分布表,并求出相应频率分布直方图中的a,b;
分组 | 频数 | 频率 |
[59.0,63.0) | 2 | 0.05 |
[63.0,67.0) | ||
[67.0,71.0) | ||
[71.0,75.0) | 9 | 0.225 |
[75.0,7.0) | 7 | 0.175 |
[79.0,83.0] | 5 | 0.125 |
合计 | 40 | 1.00 |
(2)请根据统计思想,利用(1)中的频率分布直方图估计亚洲人民的平均寿命. 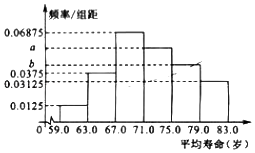
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举行“青少年禁毒”知识竞赛网上答题,高二年级共有500名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了100名学生的成绩进行统计.请你解答下列问题:
分组 | 频数 | 频率 |
[60,70) | 10 | 0.1 |
[70,80) | 22 | 0.22 |
[80,90) | a | 0.38 |
[90,100] | 30 | c |
合计 | 100 | d |

(1)根据下面的频率分布表和频率分布直方图,求出a+d和b+c的值;
(2)若成绩不低于90分的学生就能获奖,问所有参赛学生中获奖的学生约为多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p: ![]() <1,q:x2+(a﹣1)x﹣a>0,若p是q的充分不必要条件,则实数a的取值范围是( )
<1,q:x2+(a﹣1)x﹣a>0,若p是q的充分不必要条件,则实数a的取值范围是( )
A.(﹣2,﹣1]
B.[﹣2,﹣1]
C.[﹣3,﹣1]
D.[﹣2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p: ![]() <1,q:x2+(a﹣1)x﹣a>0,若p是q的充分不必要条件,则实数a的取值范围是( )
<1,q:x2+(a﹣1)x﹣a>0,若p是q的充分不必要条件,则实数a的取值范围是( )
A.(﹣2,﹣1]
B.[﹣2,﹣1]
C.[﹣3,﹣1]
D.[﹣2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为4,P为BC的中点,Q为线段CC1上的动点(异于C点),过点A,P,Q的平面截面记为M.
则当CQ∈时(用区间或集合表示),M为四边形;
当CQ=时(用数值表示),M为等腰梯形;
当CQ=4时,M的面积为 . 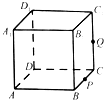
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com