已知O是锐角三角形ABC的外心,△BOC,△COA,△AOB的面积数依次成等差数列.
(1)推算tanAtanC是否为定值?说明理由;
(2)求证:tanA,tanB,tanC也成等差数列.
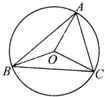
解:如图所示,设△ABC的外接圆半径为R,
则
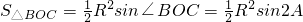
,
同理:
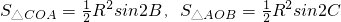
.
∵S
△BOC,S
△COA,S
△AOB成等差数列,
∴2S
△COA=S
△BOC+S
△AOB,
即
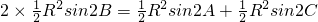
.
∴2sin2B=sin2A+sin2C,∴2sin2B=sin[(A+C)+(A-C)]+sin[(A+C)-(A-C)],
∴4sinBcosB=2sin(A+C)cos(A-C).
又A+B+C=π,故sinB=sin(A+C)≠0.
∴2cosB=cos(A-C).
又A+B+C=π,∴-2cos(A+C)=cos(A-C).
整理得 sinA•sinC=3cosA•cosC.
(1)因△ABC是锐角三角形,
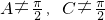
,可知cosA≠0,cosC≠0,∴tanAtanC=3,
故tanAtanC为定值.
(2)∵
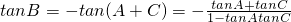
=
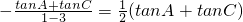
.∴2tanB=tanA+tanC,
即tanA,tanB,tanC成等差数列.
分析:如图所示,设△ABC的外接圆半径为R,则
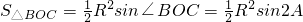
,
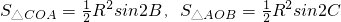
,由题意可得2S
△COA=S
△BOC+S
△AOB,整理可得2sin2B=sin2A+sin2C,结合三角形的内角和公式及和差角公式整理得 sinA•sinC=3cosA•cosC.
(1)因△ABC是锐角三角形,
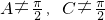
,可知cosA≠0,cosC≠0,可求tanAtanC.
(2)要证tanA,tanB,tanC成等差数列.只要证明2tanB=tanA+tanC即可
点评:本题主要以等差数列的性质为切入点,主要考查了三角形中正弦定理、两角和与差的三角公式,三角形的内角和公式等知识的综合应用.

 解:如图所示,设△ABC的外接圆半径为R,
解:如图所示,设△ABC的外接圆半径为R,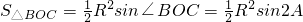 ,
,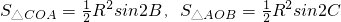 .
.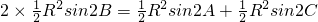 .
.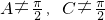 ,可知cosA≠0,cosC≠0,∴tanAtanC=3,
,可知cosA≠0,cosC≠0,∴tanAtanC=3,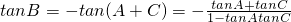 =
=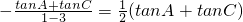 .∴2tanB=tanA+tanC,
.∴2tanB=tanA+tanC,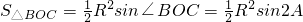 ,
,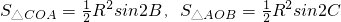 ,由题意可得2S△COA=S△BOC+S△AOB,整理可得2sin2B=sin2A+sin2C,结合三角形的内角和公式及和差角公式整理得 sinA•sinC=3cosA•cosC.
,由题意可得2S△COA=S△BOC+S△AOB,整理可得2sin2B=sin2A+sin2C,结合三角形的内角和公式及和差角公式整理得 sinA•sinC=3cosA•cosC.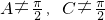 ,可知cosA≠0,cosC≠0,可求tanAtanC.
,可知cosA≠0,cosC≠0,可求tanAtanC.

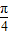 ,若
,若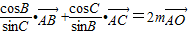 ,则m,的值为( )
,则m,的值为( )
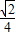

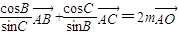 ,则m=( )
,则m=( )