
【题目】已知数列{an}(n∈N*)是公差不为0的等差数列,a1=1,且 ![]() ,
, ![]() ,
, ![]() 成等比数列.
成等比数列.
(1)求数列{an}的通项公式;
(2)设数列{ ![]() }的前n项和为Tn , 求证:Tn<1.
}的前n项和为Tn , 求证:Tn<1.
【答案】
(1)解:设{an}的公差为d.
因为 ![]() 成等比数列,所以
成等比数列,所以 ![]() .
.
即 ![]() .
.
化简得 ![]() ,即d2=a1d.
,即d2=a1d.
又a1=1,且d≠0,解得d=1.
所以有an=a1+(n﹣1)d=n.
(2)解:由(1)得: ![]() .
.
所以 ![]() .
.
因此,Tn<1
【解析】(1)利用已知列出关于工程师了公差方程求出公差;得到通项公式;(2)利用(1)的结论,将通项公式代入,利用裂项求和证明即可.
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系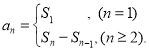 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】如今,中国的“双十一”已经从一个节日变成了全民狂欢的“电商购物日”.某淘宝电商分析近8年“双十一”期间的宣传费用![]() (单位:万元)和利润
(单位:万元)和利润![]() (单位:十万元)之间的关系,得到下列数据:
(单位:十万元)之间的关系,得到下列数据:
| 2 | 3 | 4 | 5 | 6 | 8 | 9 | 11 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
请回答:
(Ⅰ)请用相关系数![]() 说明
说明![]() 与
与![]() 之间是否存在线性相关关系(当
之间是否存在线性相关关系(当![]() 时,说明
时,说明![]() 与
与![]() 之间具有线性相关关系);
之间具有线性相关关系);
(Ⅱ)根据1的判断结果,建立![]() 与
与![]() 之间的回归方程,并预测当
之间的回归方程,并预测当![]() 时,对应的利润
时,对应的利润![]() 为多少(
为多少(![]() 精确到
精确到![]() ).
).
附参考公式:回归方程中![]() 中
中![]() 和
和![]() 最小二乘估计分别为
最小二乘估计分别为 ,
,![]() ,
,
相关系数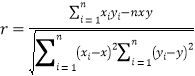 .
.
参考数据: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是无穷数列,满足lgan+1=|lgan﹣lgan﹣1|(n=2,3,4,…).
(1)若a1=2,a2=3,求a3 , a4 , a5的值;
(2)求证:“数列{an}中存在ak(k∈N*)使得lgak=0”是“数列{an}中有无数多项是1”的充要条件;
(3)求证:在数列{an}中ak(k∈N*),使得1≤ak<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 且
且![]() ,设命题
,设命题![]() :函数
:函数![]() 在
在![]() 上单调递减,命题
上单调递减,命题![]() :对任意实数
:对任意实数![]() ,不等式
,不等式![]() 恒成立.
恒成立.
(1)写出命题![]() 的否定,并求非
的否定,并求非![]() 为真时,实数
为真时,实数![]() 的取值范围;
的取值范围;
(2)如果命题“![]() ”为真命题,且“
”为真命题,且“![]() ”为假命题,求实数
”为假命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知A,B,C,D四点共面,且CD=1,BC=2,AB=4,∠ABC=120°,cos∠BDC= ![]() .
. 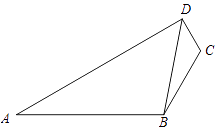
(1)求sin∠DBC;
(2)求AD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(﹣![]() ,0)和B(
,0)和B(![]() ,0),动点C到A、B两点的距离之差的绝对值为2.
,0),动点C到A、B两点的距离之差的绝对值为2.
(1)求点C的轨迹方程;
(2)点C的轨迹与经过点(2,0)且斜率为1的直线交于D、E两点,求线段DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com