
| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 20 | D. | 5 |
分析 设z2=2+ai,a∈R,又z1=1-2i,由复数代数形式的乘除运算求出a,则复数z2可求,进一步求出$\overline{{z}_{2}}$,则z2•$\overline{{z}_{2}}$可求.
解答 解:设z2=2+ai,a∈R,
又z1=1-2i,
则z1•z2=(1-2i)•(2+ai)=(2+2a)+(a-4)i.
∵z1•z2是实数,
∴a-4=0.
∴a=4.
∴z2=2+4i.$\overline{{z}_{2}}=2-4i$.
则z2•$\overline{{z}_{2}}$=(2+4i)•(2-4i)=20.
故选:C.
点评 本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{π}{4}$-$\frac{1}{2}$ | C. | $\frac{π}{4}$ | D. | 1-$\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
| 态度 年龄 | 赞成 | 不赞成 | 总计 |
| 中青年 | |||
| 中老年 | |||
| 总计 |
| X2 | ≤2.706 | >2.706 | >3.841 | >6.635 |
| A、B关联性 | 无关联 | 90% | 95% | 99% |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=g(x)在(0,$\frac{π}{2}$)上递减 | B. | y=g(x)在(0,$\frac{π}{6}$)上递减 | ||
| C. | y=g(x)在(0,$\frac{π}{2}$)上递增 | D. | y=g(x)在(0,$\frac{π}{6}$)上递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
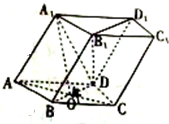 在四棱柱ABCD一A1B1C1D1中,底面ABCD是菱形,且AB=AA1=$\sqrt{5}$,BD=4,A1在底面 ABCD的射影是AC与BD的交点O.
在四棱柱ABCD一A1B1C1D1中,底面ABCD是菱形,且AB=AA1=$\sqrt{5}$,BD=4,A1在底面 ABCD的射影是AC与BD的交点O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com