
【题目】已知函![]() 数是奇函数,且f(2)=
数是奇函数,且f(2)=![]() .
.
(1)求实数m和n的值;
(2)求函数f(x)在区间[-2,-1]上的最值.
【答案】(1)实数m和n的值分别是2和0;(2)![]() .
.
【解析】试题分析: 已知函数的奇偶性求函数的解析式是函数的奇偶性常见考试题,由于函数是奇函数,则![]() ,又f(2)=
,又f(2)= ![]() ,列方程组解出m,n,求出函数的解析式,有了函数的解析式可以利用定义研究函数的单调性,也可借助对勾函数研究函数的单调性,也可借助导数研究函数的单调性,进而求函数在某区间上的最值.
,列方程组解出m,n,求出函数的解析式,有了函数的解析式可以利用定义研究函数的单调性,也可借助对勾函数研究函数的单调性,也可借助导数研究函数的单调性,进而求函数在某区间上的最值.
试题解析:
(1)∵f(x)是奇函数,∴f(-x)=-f(x),
∴![]() .
.
比较得n=-n,n=0.
又f(2)=![]() ,∴
,∴![]() ,解得m=2.
,解得m=2.
因此,实数m和n的值分别是2和0.
(2)由(1)知f(x)=![]() .
.
任取x1,x2∈[-2,-1],且x1<x2,
则f(x1)-f(x2)=![]() (x1-x2)
(x1-x2) 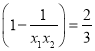 (x1-x2)·
(x1-x2)·![]() .
.
∵-2≤x1<x2≤-1时,
∴x1-x2<0,x1x2>0,x1x2-1>0,
∴f(x1)-f(x2)<0,即f(x1)<f(x2).
∴函数f(x)在[-2,-1]上为增函数,
因此f(x)max=f(-1)=-![]() ,f(x)min=f(-2)=-
,f(x)min=f(-2)=-![]() .
.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=lg(ax﹣bx),且f(1)=lg2,f(2)=lg12
(1)求a,b的值.
(2)当x∈[1,2]时,求f(x)的最大值.
(3)m为何值时,函数g(x)=ax的图象与h(x)=bx﹣m的图象恒有两个交点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某出租车公司为了解本公司出租车司机对新法规的知晓情况,随机对![]() 名出租车司机进行调查,调查问卷共
名出租车司机进行调查,调查问卷共![]() 道题,答题情况如下表:
道题,答题情况如下表:
答对题目数 |
|
|
|
|
女 |
|
|
|
|
男 |
|
|
|
|
(I)如果出租车司机答对题目大于等于![]() ,就认为该司机对新法规的知晓情况比较好,试估计该公司的出租车司机对新法规知晓情况比较好的概率;
,就认为该司机对新法规的知晓情况比较好,试估计该公司的出租车司机对新法规知晓情况比较好的概率;
(II)从答对题目数小于![]() 的出租车司机中选出
的出租车司机中选出![]() 人做进一步的调查,求选出的
人做进一步的调查,求选出的![]() 人中至少有一名女出租车司机的概率.
人中至少有一名女出租车司机的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com