
【题目】对于定义域为D的函数![]() ,若存在区间
,若存在区间![]() ,使得
,使得![]() 同时满足,①
同时满足,①![]() 在
在![]() 上是单调函数,②当
上是单调函数,②当![]() 的定义域为
的定义域为![]() 时,
时,![]() 的值域也为
的值域也为![]() ,则称区间
,则称区间![]() 为该函数的一个“和谐区间”
为该函数的一个“和谐区间”
(1)求出函数![]() 的所有“和谐区间”
的所有“和谐区间”![]() ;
;
(2)函数![]() 是否存在“和谐区间”
是否存在“和谐区间”![]() ?若存在,求出实数a,b的值;若不存在,请说明理由
?若存在,求出实数a,b的值;若不存在,请说明理由
(3)已知定义在![]() 上的函数
上的函数![]() 有“和谐区间”,求正整数k取最小值时实数m的取值范围.
有“和谐区间”,求正整数k取最小值时实数m的取值范围.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)不存在;理由见解析;(3)
;(2)不存在;理由见解析;(3)![]()
【解析】
(1)根据“和谐”函数的定义,建立条件关系,即可求![]() 符合条件的“和谐”区间;
符合条件的“和谐”区间;
(2)判断函数![]() 是否满足“和谐”函数的条件即可;
是否满足“和谐”函数的条件即可;
(3)根据函数![]() 是“和谐”函数,建立条件关系,即可求实数
是“和谐”函数,建立条件关系,即可求实数![]() 的取值范围.
的取值范围.
(1)因为函数![]() 在
在![]() 上单调递增,
上单调递增,
所以有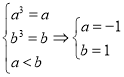 或
或![]() 或
或![]() ;
;
即![]() 或
或![]() 或
或![]() .
.
(2)画出函数![]() 的图象
的图象
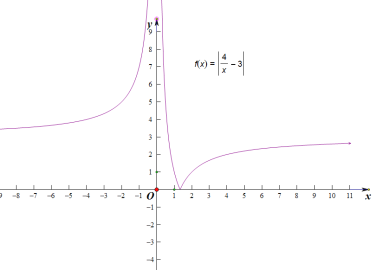
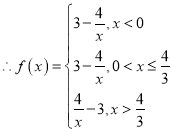
由图可知函数在![]() ,
,![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
且函数值域为![]() ,故在
,故在![]() 上不存在 “和谐区间”;
上不存在 “和谐区间”;
假设函数在区间![]() 存在 “和谐区间”
存在 “和谐区间”![]() ,则
,则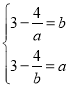 方程组无解,假设不成立;同理可得函数在区间
方程组无解,假设不成立;同理可得函数在区间![]() 也不存在 “和谐区间”。
也不存在 “和谐区间”。
故函数![]() 不存在 “和谐区间”。
不存在 “和谐区间”。
(3)![]() 在
在![]() 上有“和谐区间”,
上有“和谐区间”,
所以存在区间![]() ,使函数
,使函数![]() 的值域为
的值域为![]() ,
,
![]() 函数在
函数在![]() 上单调递增
上单调递增
![]() 在
在![]() 单调递增,即
单调递增,即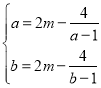 ,
,
![]() 为关于
为关于![]() 的方程
的方程![]() 的两个实根,即方程
的两个实根,即方程![]() 在
在![]() 上有两个不等的实根,即
上有两个不等的实根,即![]() 在
在![]() 上有两个不等的实根,令
上有两个不等的实根,令![]()
与![]() ,问题转化为函数
,问题转化为函数![]() 与
与![]() ,在
,在![]() 上存在两个不同的交点.
上存在两个不同的交点.
考察函数![]() 如图
如图
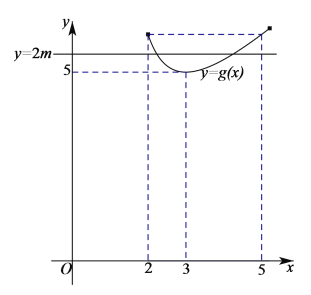
函数![]() 在
在![]() 单调递减,在
单调递减,在![]() 上单调递增.
上单调递增.
![]() ,且
,且![]() ,
,
∵函数![]() 在
在![]() 上递减,当
上递减,当![]() 时,直线
时,直线![]() 与函数
与函数![]() 不可能有两个交点,∴
不可能有两个交点,∴![]()
∵![]() 在
在![]() 递增,由图象可知,当
递增,由图象可知,当![]() 时,函数
时,函数![]() 与
与![]() 在
在![]() 存在两个交点,
存在两个交点,
所以正整数![]() 的最小值为
的最小值为![]() ,
,![]() ,此时,
,此时,![]() ,解得
,解得![]() .
.
故![]() .
.


科目:高中数学 来源: 题型:
【题目】【2018山西晋城市高三上学期一模】环境问题是当今世界共同关注的问题,我国环保总局根据空气污染指数![]() 浓度,制定了空气质量标准:
浓度,制定了空气质量标准:
空气污染指数 |
|
|
|
|
|
|
空气质量等级 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
某市政府为了打造美丽城市,节能减排,从2010年开始考察了连续六年11月份的空气污染指数,绘制了频率分布直方图,经过分析研究,决定从2016年11月1日起在空气质量重度污染和严重污染的日子对机动车辆限号出行,即车牌尾号为单号的车辆单号出行,车牌尾号为双号的车辆双号出行(尾号是字母的,前13个视为单号,后13个视为双号),王先生有一辆车,若11月份被限行的概率为0.05.
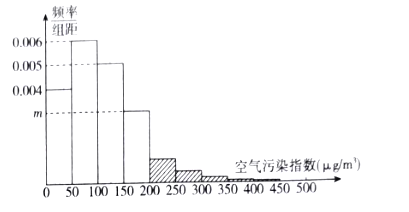
(I)求频率分布直方图中![]() 的值(写出推理过程,直接写出答案不得分);
的值(写出推理过程,直接写出答案不得分);
(II)若按分层抽样的方法,从空气质量良好与中度污染的天气中抽取6天,再从这6天中随机抽取2天,求至少有一天空气质量中度污染的概率;
(III)该市环保局为了调查汽车尾气排放对空气质量的影响,对限行两年来的11月份共60天的空气质量进行统计,其结果如下表:

根据限行前6年180天与限行后60天的数据,计算并填写以下![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为空气质量的优良与汽车尾气的排放有关.
的把握认为空气质量的优良与汽车尾气的排放有关.

参考数据:

参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“双十二”是继“双十一”之后的又一个网购狂欢节,为了刺激“双十二”的消费,某电子商务公司决定对“双十一”的网购者发放电子优惠券.为此,公司从“双十一”的网购消费者中用随机抽样的方法抽取了100人,将其购物金额(单位:万元)按照![]() ,
, ![]() 分组,得到如下频率分布直方图:
分组,得到如下频率分布直方图:
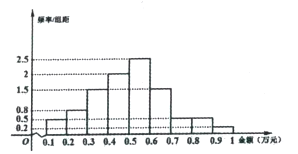
根据调查,该电子商务公司制定了发放电子优惠券的办法如下:

(Ⅰ)求购物者获得电子优惠券金额的平均数;
(Ⅱ)从这100名购物金额不少于0.8万元的人中任取2人,求这两人的购物金额在0.8~0.9万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家电公司根据销售区域将销售员分成![]() ,
,![]() 两组.
两组.![]() 年年初,公司根据销售员的销售业绩分发年终奖,销售员的销售额(单位:十万元)在区间
年年初,公司根据销售员的销售业绩分发年终奖,销售员的销售额(单位:十万元)在区间![]() ,
,![]() ,
,![]() ,
,![]() 内对应的年终奖分别为2万元,2.5万元,3万元,3.5万元.已知销售员的年销售额都在区间
内对应的年终奖分别为2万元,2.5万元,3万元,3.5万元.已知销售员的年销售额都在区间![]() 内,将这些数据分成4组:
内,将这些数据分成4组:![]() ,
,![]() ,
,![]() ,
,![]() ,得到如下两个频率分布直方图:
,得到如下两个频率分布直方图:
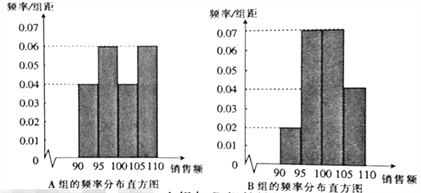
以上面数据的频率作为概率,分别从![]() 组与
组与![]() 组的销售员中随机选取1位,记
组的销售员中随机选取1位,记![]() ,
,![]() 分别表示
分别表示![]() 组与
组与![]() 组被选取的销售员获得的年终奖.
组被选取的销售员获得的年终奖.
(1)求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)试问![]() 组与
组与![]() 组哪个组销售员获得的年终奖的平均值更高?为什么?
组哪个组销售员获得的年终奖的平均值更高?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】暑假期间,某旅行社为吸引游客去某风景区旅游,推出如下收费标准:若旅行团人数不超过30,则每位游客需交费用600元;若旅行团人数超过30,则游客每多1人,每人交费额减少10元,直到达到70人为止.
(1)写出旅行团每人需交费用![]() (单位:元)与旅行团人数
(单位:元)与旅行团人数![]() 之间的函数关系式;
之间的函数关系式;
(2)旅行团人数为多少时,旅行社可以从该旅行团获得最大收入?最大收入是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com