
【题目】将函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度,再向上平移1个单位长度,得到函数
个单位长度,再向上平移1个单位长度,得到函数![]() 的图象,则函数
的图象,则函数![]() 具有性质__________.(填入所有正确性质的序号)
具有性质__________.(填入所有正确性质的序号)
①最大值为![]() ,图象关于直线
,图象关于直线![]() 对称;
对称;
②图象关于![]() 轴对称;
轴对称;
③最小正周期为![]() ;
;
④图象关于点![]() 对称;
对称;
⑤在![]() 上单调递减
上单调递减
【答案】②③④
【解析】将函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度,得到
个单位长度,得到![]()
![]() 的图象向上平移
的图象向上平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,对于函数
的图象,对于函数![]() :它的最大值为
:它的最大值为![]() ,由于当
,由于当![]() 时,
时,![]() ,不是最值,故
,不是最值,故![]() 图象不关于直线
图象不关于直线![]() 对称,故排除①;由于该函数为偶函数,故它的图象关于
对称,故排除①;由于该函数为偶函数,故它的图象关于![]() 轴对称,故②正确;它的最小周期为
轴对称,故②正确;它的最小周期为![]() ,故③正确;当
,故③正确;当![]() 时,
时,![]() ,故函数的图象关于点
,故函数的图象关于点![]() 对称,故正④确;在
对称,故正④确;在![]() 上,
上,![]() 不是单调函数,故排除⑤,故答案为②③④.
不是单调函数,故排除⑤,故答案为②③④.
【方法点晴】本题主要考查三角函数的单调性、三角函数的周期性及奇偶性,属于难题.三角函数的图象与性质是高考考查的热点之一,经常考查定义域、值域、周期性、对称性、奇偶性、单调性、最值等,其中公式运用及其变形能力、运算能力、方程思想等可以在这些问题中进行体现,在复习时要注意基础知识的理解与落实.三角函数的性质由函数的解析式确定,在解答三角函数性质的综合试题时要抓住函数解析式这个关键,在函数解析式较为复杂时要注意使用三角恒等变换公式把函数解析式化为一个角的一个三角函数形式,然后利用正弦(余弦)函数的性质求解.


科目:高中数学 来源: 题型:
【题目】某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数,得到如下资料:

(1)从3月1日至3月5日中任选2天,记发芽的种子数分别为![]() ,求事件“
,求事件“![]() 均小于25”的概率;
均小于25”的概率;
(2)请根据3月2日至3月4日的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(参考公式:回归直线方程为![]() ,其中
,其中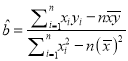 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列说法:①球的半径是球面上任意一点与球心的连线;②球的直径是球面上任意两点的连线;③用一个平面截一个球面,得到的是一个圆;④球常用表示球心的字母表示.
其中说法正确的是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:存在实数m,使方程x2+mx+1=0有两个不等的负根;命题q:存在实数m,使方程4x2+4(m-2)x+1=0无实根.若“p或q”为真,“p且q”为假,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司过去五个月的广告费支出![]() 与销售额
与销售额![]() (单位:万元)之间有下列对应数据:
(单位:万元)之间有下列对应数据:
| 2 | 4 | 5 | 6 | 8 |
|
| 40 | 60 | 50 | 70 |
工作人员不慎将表格中![]() 的第一个数据丢失.已知
的第一个数据丢失.已知![]() 对
对![]() 呈线性相关关系,且回归方程为
呈线性相关关系,且回归方程为![]() ,则下列说法:①销售额
,则下列说法:①销售额![]() 与广告费支出
与广告费支出![]() 正相关;②丢失的数据(表中
正相关;②丢失的数据(表中![]() 处)为30;③该公司广告费支出每增加1万元,销售额一定增加
处)为30;③该公司广告费支出每增加1万元,销售额一定增加![]() 万元;④若该公司下月广告投入8万元,则销售
万元;④若该公司下月广告投入8万元,则销售
额为70万元.其中,正确说法有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙两地相距为![]() 千米,汽车从甲地匀速行驶到乙地,速度每小时不超过
千米,汽车从甲地匀速行驶到乙地,速度每小时不超过![]() 千米.已知汽车每小时的运输成本(单位:元)由可变部分和固定部分组成:固定部分为
千米.已知汽车每小时的运输成本(单位:元)由可变部分和固定部分组成:固定部分为![]() 元,可变部分与速度
元,可变部分与速度![]() (单位;
(单位; ![]() )的平方成正比,且比例系数为
)的平方成正比,且比例系数为![]() .
.
(1)求汽车全程的运输成本![]() (单位:元)关于速度
(单位:元)关于速度![]() (单位;
(单位; ![]() )的函数解析式;
)的函数解析式;
(2)为了全程的运输成本最小,汽车应该以多大的速度行驶?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人练习罚球,每人练习6组,每组罚球20个,命中个数的茎叶图如下:

(1)求甲命中个数的中位数和乙命中个数的众数;
(2)通过计算,比较甲乙两人的罚球水平.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第![]() 届夏季奥林匹克运动会2016年8月5日到2016年8月21日在巴西里约热内卢举行,为了解我校学生“收看奥运会足球赛”是否与性別有关,从全校学生中随机抽取
届夏季奥林匹克运动会2016年8月5日到2016年8月21日在巴西里约热内卢举行,为了解我校学生“收看奥运会足球赛”是否与性別有关,从全校学生中随机抽取![]() 名进行了问卷调查,得到
名进行了问卷调查,得到![]() 列联表,从这
列联表,从这![]() 名同学中随机抽取
名同学中随机抽取![]() 人,抽到“收看奥运会足球赛 ”的学生的概率是
人,抽到“收看奥运会足球赛 ”的学生的概率是![]() .
.
男生 | 女生 | 合计 | |
收看 |
| ||
不收看 |
| ||
合计 |
|
(1)请将上面的![]() 列联表补充完整,并据此资料分析“收看奥运会足球赛”与性別是否有关;
列联表补充完整,并据此资料分析“收看奥运会足球赛”与性別是否有关;
(2)若从这![]() 名同学中的男同学中随机抽取
名同学中的男同学中随机抽取![]() 人参加有奖竞猜活动,记抽到收看奥运会足球赛”的学生人数为
人参加有奖竞猜活动,记抽到收看奥运会足球赛”的学生人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式:
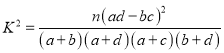 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com