
【题目】已知![]() .
.
(1)若关于![]() 的方程
的方程![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的值;
的值;
(2)证明:当![]() 时,
时, ![]() .
.
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:高中数学 来源: 题型:
【题目】(导学号:05856299)已知双曲线![]() (a>0,b>0)的左、右焦点分别是F1,F2,点P是其上一点,双曲线的离心率是2,若△F1PF2是直角三角形且面积为3,则双曲线的实轴长为( )
(a>0,b>0)的左、右焦点分别是F1,F2,点P是其上一点,双曲线的离心率是2,若△F1PF2是直角三角形且面积为3,则双曲线的实轴长为( )
A. 2 B. ![]() C. 2或
C. 2或![]() D. 1或
D. 1或![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某读者协会为了了解该地区居民睡前看书的时间情况,从该地区睡前看书的居民中随机选取了n人进行调查,现将调查结果进行统计得到如图所示的频率分布直方图.则下列说法正确的是( )

A. 睡前看书时间介于40~50分钟的频率为0.03
B. 睡前看书时间低于30分钟的频率为0.67
C. 若n=1000,则可估计本次调查中睡前看书时间介于30~50分钟的有67人
D. 若n=1000,则可估计本次调查中睡前看书时间介于20~40分钟的有600人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex-ax2(x∈R),e=2.718 28…为自然对数的底数.
(1)求函数f(x)在点P(0,1)处的切线方程;
(2)若函数f(x)为R上的单调递增函数,试求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在标准温度和大气压下,人体血液中氢离子的物质的量的浓度(单位mol/L,记作![]() )和氢氧根离子的物质的量的浓度(单位mol/L,记作
)和氢氧根离子的物质的量的浓度(单位mol/L,记作![]() )的乘积等于常数
)的乘积等于常数![]() .已知pH值的定义为
.已知pH值的定义为![]() ,健康人体血液的pH值保持在7.35~7.45之间,那么健康人体血液中的
,健康人体血液的pH值保持在7.35~7.45之间,那么健康人体血液中的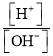 可以为(参考数据:
可以为(参考数据: ![]() ,
, ![]() )
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)为定义在R上的偶函数,当x≥0时,有f(x+1)=-f(x),且当x∈[0,1)时,f(x)=log2(x+1),给出下列命题
①f(2014)+f(-2015)=0;
②函数f(x)在定义域上是周期为2的函数;
③直线y=x与函数f(x)的图象有2个交点;
④函数f(x)的值域为(-1,1).
其中正确的是( )
A. ①② B. ②③
C. ①④ D. ①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,直线
的焦点为F,直线![]() 与x轴的交点为P,与抛物线的交点为Q,且
与x轴的交点为P,与抛物线的交点为Q,且![]() .
.
(1)求抛物线的方程;
(2)过F的直线l与抛物线相交于A,D两点,与圆![]() 相交于B,C两点(A,B两点相邻),过A,D两点分别作抛物线的切线,两条切线相交于点M,求△ABM与△CDM的面积之积的最小值.
相交于B,C两点(A,B两点相邻),过A,D两点分别作抛物线的切线,两条切线相交于点M,求△ABM与△CDM的面积之积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com