
”¾ĢāÄæ”æij¾°ĒųŠŽ½ØŅ»¶°ø“¹Å½ØÖž£¬Ęä“°»§Éč¼ĘČēĶ¼ĖłŹ¾£®Ō²![]() µÄŌ²ŠÄÓė¾ŲŠĪ
µÄŌ²ŠÄÓė¾ŲŠĪ![]() ¶Ō½ĒĻߵĽ»µćÖŲŗĻ£¬ĒŅŌ²Óė¾ŲŠĪÉĻĻĀĮ½±ßĻąĒŠ(
¶Ō½ĒĻߵĽ»µćÖŲŗĻ£¬ĒŅŌ²Óė¾ŲŠĪÉĻĻĀĮ½±ßĻąĒŠ(![]() ĪŖÉĻĒŠµć)£¬Óė×óÓŅĮ½±ßĻą½»(
ĪŖÉĻĒŠµć)£¬Óė×óÓŅĮ½±ßĻą½»(![]() £¬
£¬ ![]() ĪŖĘäÖŠĮ½øö½»µć)£¬Ķ¼ÖŠŅõÓ°²æ·ÖĪŖ²»Ķø¹āĒųÓņ£¬ĘäÓą²æ·ÖĪŖĶø¹āĒųÓņ£®ŅŃÖŖŌ²µÄ°ė¾¶ĪŖ1m£¬ĒŅ
ĪŖĘäÖŠĮ½øö½»µć)£¬Ķ¼ÖŠŅõÓ°²æ·ÖĪŖ²»Ķø¹āĒųÓņ£¬ĘäÓą²æ·ÖĪŖĶø¹āĒųÓņ£®ŅŃÖŖŌ²µÄ°ė¾¶ĪŖ1m£¬ĒŅ![]() £®Éč
£®Éč![]() £¬Ķø¹āĒųÓņµÄĆ껿ĪŖ
£¬Ķø¹āĒųÓņµÄĆ껿ĪŖ![]() £®
£®
£Ø1£©Ēó![]() ¹ŲÓŚ
¹ŲÓŚ![]() µÄŗÆŹż¹ŲĻµŹ½£¬²¢Ēó³ö¶ØŅåÓņ£»
µÄŗÆŹż¹ŲĻµŹ½£¬²¢Ēó³ö¶ØŅåÓņ£»
£Ø2£©øł¾ŻÉč¼ĘŅŖĒó£¬Ķø¹āĒųÓņÓė¾ŲŠĪ“°ĆęµÄĆ껿±ČÖµŌ½“óŌ½ŗĆ£®µ±øƱČÖµ×ī“óŹ±£¬Ēó±ß![]() µÄ³¤¶Č£®
µÄ³¤¶Č£®
”¾“š°ø”æ£Ø1£©£Ø2£©
”¾½āĪö”æŹŌĢā·ÖĪö: øł¾ŻĢāŅā±ķŹ¾³öĖłŠčµÄĻ߶Ī³¤¶Č£¬ŌŁ·Ö±šĒóČż½ĒŠĪŗĶÉČŠĪĆ껿£¬“Ó¶ų±ķŹ¾³ö×ÜĆ껿£¬ŌŁøł¾ŻĢāŅāŅŖĒóĒó³öŗÆŹżµÄ¶ØŅåÓņ£»øł¾ŻĢāŅā±ķŹ¾³ö”°Ķø¹ā±Č”±ŗÆŹż![]() £¬½čÖśĒóµ¼£¬ŃŠ¾æŗÆŹżµ„µ÷ŠŌĒó³ö×ī“óÖµ.
£¬½čÖśĒóµ¼£¬ŃŠ¾æŗÆŹżµ„µ÷ŠŌĒó³ö×ī“óÖµ.
ŹŌĢā½āĪö:£Ø1£©¹żµć![]() ×÷
×÷![]() ÓŚµć
ÓŚµć![]() £¬Ōņ
£¬Ōņ![]() £¬
£¬
ĖłŅŌ![]() £¬
£¬
![]() £®
£®
ĖłŅŌ![]() £¬
£¬
ŅņĪŖ![]() £¬ĖłŅŌ
£¬ĖłŅŌ![]() £¬ĖłŅŌ¶ØŅåÓņĪŖ
£¬ĖłŅŌ¶ØŅåÓņĪŖ![]() £®
£®
£Ø2£©¾ŲŠĪ“°ĆęµÄĆ껿ĪŖ![]() £®
£®
ŌņĶø¹āĒųÓņÓė¾ŲŠĪ“°ĆęµÄĆ껿±ČÖµĪŖ![]() £®”10·Ö
£®”10·Ö
Éč![]() £¬
£¬ ![]() £®
£®
Ōņ![]()
 £¬
£¬
ŅņĪŖ![]() £¬ĖłŅŌ
£¬ĖłŅŌ![]() £¬ĖłŅŌ
£¬ĖłŅŌ![]() £¬¹Ź
£¬¹Ź![]() £¬
£¬
ĖłŅŌŗÆŹż![]() ŌŚ
ŌŚ![]() ÉĻµ„µ÷¼õ£®
ÉĻµ„µ÷¼õ£®
ĖłŅŌµ±![]() Ź±£¬
Ź±£¬ ![]() ÓŠ×ī“óÖµ
ÓŠ×ī“óÖµ![]() £¬“ĖŹ±
£¬“ĖŹ±![]() (m)£®
(m)£®
“š£ŗ£Ø1£©![]() ¹ŲÓŚ
¹ŲÓŚ![]() µÄŗÆŹż¹ŲĻµŹ½ĪŖ
µÄŗÆŹż¹ŲĻµŹ½ĪŖ![]() £¬¶ØŅåÓņĪŖ
£¬¶ØŅåÓņĪŖ![]() £»
£»
£Ø2£©Ķø¹āĒųÓņÓė¾ŲŠĪ“°ĆęµÄĆ껿±ČÖµ×ī“óŹ±£¬ ![]() µÄ³¤¶ČĪŖ1m£®
µÄ³¤¶ČĪŖ1m£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÓŠĮ½øö“ü×Ó£¬ĘäÖŠ¼×“ü֊װӊ±ąŗÅ·Ö±šĪŖ1”¢2”¢3”¢4µÄ4øöĶźČ«ĻąĶ¬µÄĒņ£¬ŅŅ“ü֊װӊ±ąŗÅ·Ö±šĪŖ2”¢4”¢6µÄ3øöĶźČ«ĻąĶ¬µÄĒņ£®
£Ø¢ń£©“Ó¼×”¢ŅŅ“ü×ÓÖŠø÷Č”Ņ»øöĒņ£¬ĒóĮ½Ēņ±ąŗÅÖ®ŗĶŠ”ÓŚ8µÄøÅĀŹ£»
£Ø¢ņ£©“ӼדüÖŠČ”2øöĒņ£¬“ÓŅŅ“üÖŠČ”Ņ»øöĒņ£¬ĒóĖłČ”³öµÄ3øöĒņÖŠŗ¬ÓŠ±ąŗÅĪŖ2µÄĒņµÄøÅĀŹ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ”ŃO£ŗx2+y2=1ŗĶ¶ØµćA£Ø2£¬1£©£¬ÓÉ”ŃOĶāŅ»µćP£Øa£¬b£©Ļņ”ŃOŅżĒŠĻßPQ£¬ĒŠµćĪŖQ£¬ĒŅĀś×ć|PQ|=|PA|£®
£Ø1£©Ē󏵏ża£¬b¼äĀś×ćµÄµČĮæ¹ŲĻµ£»
£Ø2£©ĒóĻ߶ĪPQ³¤µÄ×īŠ”Öµ£»
£Ø3£©ČōŅŌPĪŖŌ²ŠÄĖł×÷µÄ”ŃPÓė”ŃOÓŠ¹«¹²µć£¬ŹŌĒó°ė¾¶×īŠ”ÖµŹ±”ŃPµÄ·½³Ģ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ¾ŲŠĪABCDĖłŌŚĘ½ĆęÓėµČŃüÖ±½ĒČż½ĒŠĪBECĖłŌŚĘ½Ć껄Ļą“¹Ö±£¬BE”ĶEC£¬AB=BE£¬MĪŖĻ߶ĪAEµÄÖŠµć£®
£Ø¢ń£© Ö¤Ć÷£ŗBM”ĶĘ½ĆęAEC£»
£Ø¢ņ£© ĒóMCÓėĘ½ĆęDECĖł³ÉµÄ½ĒµÄÓąĻŅÖµ£®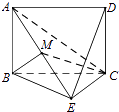
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖĖıߊĪABCDŹĒ±ß³¤ĪŖ1µÄÕż·½ŠĪ£¬PA”ĶĘ½ĆęABCD£¬NŹĒPCµÄÖŠµć£®
£Ø¢ń£©ČōPA=1£¬Ēó¶žĆę½ĒB©PC©DµÄ“󊔣»
£Ø¢ņ£©ĒóANÓėĘ½ĆęPCDĖł³É½ĒµÄÕżĻŅÖµµÄ×ī“óÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÉč¼×”¢ŅŅ”¢±ūČżøöĘ¹ÅŅĒņŠ»įµÄ·Ö±šŃ”ÅÉ3£¬1£¬2ĆūŌĖ¶ÆŌ±²Ī¼Óij“Ī±ČČü£¬¼×Š»įŌĖ¶ÆŌ±±ąŗÅ·Ö±šĪŖA1 £¬ A2 £¬ A3 £¬ ŅŅŠ»į±ąŗÅĪŖA4 £¬ ±ūŠ»į±ąŗÅ·Ö±šĪŖA5 £¬ A6 £¬ Čō“ÓÕā6ĆūŌĖ¶ÆŌ±ÖŠĖ껜³éČ”2Ćū²Ī¼ÓĖ«“ņ±ČČü£®
£Ø1£©ÓĆĖłøų±ąŗÅĮŠ³öĖłÓŠæÉÄܳéČ”µÄ½į¹ū£»
£Ø2£©Ēó±ūŠ»įÖĮÉŁÓŠŅ»ĆūŌĖ¶ÆŌ±²Ī¼ÓĖ«“ņ±ČČüµÄøÅĀŹ£»
£Ø3£©Ēó²Ī¼ÓĖ«“ņ±ČČüµÄĮ½ĆūŌĖ¶ÆŌ±Ą“×ŌĶ¬Ņ»Š»įµÄøÅĀŹ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijĄŗĒņ¶Ó¼×”¢ŅŅĮ½ĆūŌĖ¶ÆŌ±Į·Ļ°·£Ēņ£¬ĆæČĖĮ·Ļ°10×飬Ćæ×é·£Ēņ40øö£®ĆüÖŠøöŹżµÄ¾„Ņ¶Ķ¼ČēĻĀ£®ŌņĻĀĆę½įĀŪÖŠ“ķĪóµÄŅ»øöŹĒ£Ø £© 
A.¼×µÄ¼«²īŹĒ29
B.ŅŅµÄÖŚŹżŹĒ21
C.¼×·£ĒņĆüÖŠĀŹ±ČŅŅøß
D.¼×µÄÖŠĪ»ŹżŹĒ24
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŗÆŹż![]() .
.
£Ø1£©ĢÖĀŪŗÆŹż![]() µÄµ„µ÷ŠŌ£»
µÄµ„µ÷ŠŌ£»
£Ø2£©µ±![]() Ź±£¬ČōŗÆŹż
Ź±£¬ČōŗÆŹż![]() µÄµ¼ŗÆŹż
µÄµ¼ŗÆŹż![]() µÄĶ¼ĻóÓė
µÄĶ¼ĻóÓė![]() Öį½»ÓŚ
Öį½»ÓŚ![]() £¬
£¬ ![]() Į½µć£¬Ęäŗį×ų±ź·Ö±šĪŖ
Į½µć£¬Ęäŗį×ų±ź·Ö±šĪŖ![]() £¬
£¬ ![]() £¬Ļ߶Ī
£¬Ļ߶Ī![]() µÄÖŠµćµÄŗį×ų±źĪŖ
µÄÖŠµćµÄŗį×ų±źĪŖ![]() £¬ĒŅ
£¬ĒŅ![]() £¬
£¬ ![]() Ē”ĪŖŗÆŹż
Ē”ĪŖŗÆŹż![]() µÄĮćµć£¬ĒóÖ¤£ŗ
µÄĮćµć£¬ĒóÖ¤£ŗ ![]() .
.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æø£Ąū²ŹĘ±”°Ė«É«Ēņ”±ÖŠŗģĒņµÄŗÅĀėæÉŅŌ“Ó01£¬02£¬03£¬”£¬32£¬33Õā33øö¶žĪ»ŗÅĀė֊єȔ£¬Š”Ć÷ĄūÓĆČēĶ¼ĖłŹ¾µÄĖ껜Źż±ķєȔŗģÉ«ĒņµÄ6øöŗÅĀė£¬Ń”Č”·½·ØŹĒ“ÓµŚ1ŠŠµŚ9ĮŠŗĶµŚ10ĮŠµÄŹż×ÖæŖŹ¼“Ó×óµ½ÓŅŅĄ“ĪєȔĮ½øöŹż×Ö£¬ŌņµŚĖÄøö±»Ń”ÖŠµÄŗģÉ«ĒņŗÅĀėĪŖ£Ø £©
81 47 23 68 63 93 17 90 12 69 86 81 62 93 50 60 91 33 75 85 61 39 85 |
06 32 35 92 46 22 54 10 02 78 49 82 18 86 70 48 05 46 88 15 19 20 49 |
A. 12 B. 33 C. 06 D. 16
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com