Question

(08年绍兴一中三模理 ) （15分）  定义：  ()

    ⑴设函数，求函数的最小值；

    ⑵解关于的不等式：

    ⑶设，正项数列满足：，；求数列的通项公式，并求所有可能乘积（）的和。

Answer 1

解析：本小题主要考查函数、数列、不等式等基础知识，考查应用数学知识分析问题和解决问题的能力，考查分类讨论等数学思想方法．

解法一：(Ⅰ)f(n)= , 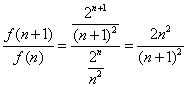．．．．．．．．．．．．．．．2分

因为2n²-(n+1)²=(n-1)²-2，

当n≥3时，(n-1)²-2>0，所以当n≥3时f(n+1)>f(n)；

当，n<3时，(n-1)²-2<O，所以当n<3时f(n+1)<f(n)．

所以当n=3时f(n)取到最小值为f(3)=．．．．．．．．．．．．．．．．．4分

 (Ⅱ)原不等式等价于不等式组即5分

(i)当a>1时，2<a+1<2a，原不等式的解集是{x|a+1<x≤2a}．…………6分

(ii)当a=l时，2a=a+1=2，原不等式的解集是空集．…………………7分

(iii)当a<1时，2a<a+1<2，原不等式的解集为{x|a+1<x≤2}．…………8分

综上，a>1时，原不等式的解集是(a+1，2a]；a=1时，原不等式的解集是；

a<l时，原不等式的解集是(a+1，2]．………………………………………9分

(Ⅲ)因为g(x)=2^x,所以g(a_n+1)= ,又g(a_n+1)= = ,

            所以a_n+1=3a_n.又a₁=3, 所以数列{a_n}是首项a₁=3，公比为3的等比数列，

所以a_n=3?3 ^n-1=3 ⁿ. ………………………………………………………10分

            记数列{3 ⁿ}的所有可能的乘积(1≤i≤j≤n)的和为S，则

S=a₁?a₁+(a₁+a₂) ?a₂+…+(a₁+a₂+…+a_n) ?a_n………………………………11分

= 3?3¹+(3+3²) ?3²+…+(3+3²+…+3ⁿ) ?3ⁿ…………………………………12分

=

= +

=

= ……………………………………………15分

解法二：(Ⅰ)由f(n)= ，计算得：

据此猜想n=3时,f(n)取到最小值．………………………………………2分

以下用数学归纳法证明n≥5时,n²<2 ⁿ成立．

(i)当n=5时，5²<2 ⁵，不等式成立．

(ii)假设n=k(k≥5)时不等式成立，即k²>2 ^k

那么2^k+1=2 ^k ?2>k² ?2 ,

因为k≥5,所以2k²-(k+1)²=k²-2k-1=(k-1)²-2>0.

所以2^k+1>(k+1)².即当n=k+1时，不等式也成立．

根据(i)和(ii)所述，对于所有n≥5，n∈N ^*，n²<2 ⁿ都成立．

结合上表可知猜想正确，即当n=3时f(n)取到最小值为f(3)=.………4分

(Ⅱ)同解法一．

(Ⅲ)同解法一，得a_n=3ⁿ.………………………………………………………10分

           由a_i?a_j=3ⁱ?3^j=3^i+j  (1≤i≤j≤n)，列表如下：

记数列{3ⁿ}的所有可能的乘积(1≤i≤j≤n)的和为S，将这个“上三角形”表绕“对角线”对称地填在“下三角形”中，得到正方形数表：

记第一行的和为S₁，那么2S一(3²+3⁴+3⁶+…+3²ⁿ)=S₁(1+3+3²+…+3^n-1).

所以2S =(3 ⁿ-1)(1+3+3²+…+3 ^n-1)+(9 ⁿ -1),

所以S =

解法三：(Ⅰ)因为f(n)= ,设

由，

所以当时，<0，所以，在内单调递减；

当时，>0，所以，在内单调递增．……2分

所以f(n)= 的最小值只可能在n=2或n=3处取到，

注意到f(2)=1,f(3)=,所以当n=3时,f(n)取到最小值为 f(3)=.

        (Ⅱ)、(Ⅲ)同解法一．

解法四：(Ⅰ)同解法二，猜想n=3时, f(n)取到最小值．………………………………2分

            证明如下：当n≥5时，

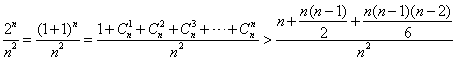
因为n≥5时，n-2≥3，

            所以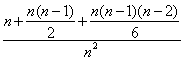≥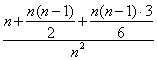=1.

结合上表可知猜想正确，即当n=3时,f(n)取到最小值为f(3)= .

(Ⅱ)(Ⅲ)同解法一．