练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知抛物线的焦点为，准线为，抛物线上存在一点，过点作，垂足为，使是等边三角形且面积为.

    （1）求抛物线的方程；

    （2）若点是圆与抛物线的一个交点，点，当取得最小值时，求此时圆的方程.

    【答案】（1）（2）

    【解析】

    （1）利用等边三角形可得值，从而得到抛物线的方程；

    （2）设的坐标为，易得，所以，结合最值即可得到圆的方程.

    解：（1）如图所示，

    ∵等边的面积为，

    设边长为，

    ∴，∴，∴

    ∵，∴

    所以抛物线的方程是.

    （2）法一：设的坐标为，因为抛物线：的焦点，

    ，

    ，

    所以当且仅当时取等号，即当取最小值时，点坐标为把点坐标代入圆的方程可得.

    法二：设的坐标为，因为抛物线：的焦点，

    ，

    ，

    所以，当且仅当时取等号，

    即当取最小值时，点坐标为

    把点坐标代入圆的方程可得.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在2018年俄罗斯世界杯期间,莫斯科的部分餐厅经营了来自中国的小龙虾,这些小龙虾标有等级代码.为得到小龙虾等级代码数值与销售单价之间的关系,经统计得到如下数据：

    等级代码数值

    38

    48

    58

    68

    78

    88

    销售单价(元

    16.8

    18.8

    20.8

    22.8

    24

    25.8

    （1）已知销售单价与等级代码数值之间存在线性相关关系,求关于的线性回归方程(系数精确到0.1)；

    （2）若莫斯科某餐厅销售的中国小龙虾的等级代码数值为98，请估计该等级的中国小龙虾销售单价为多少元？

    参考公式：对一组数据,，····,其回归直线的斜率和截距最小二乘估计分别为：,.

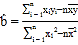    参考数据：,.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某种植物感染病毒极易导致死亡，某生物研究所为此推出了一种抗病毒的制剂，现对20株感染了病毒的该植株样本进行喷雾试验测试药效.测试结果分“植株死亡”和“植株存活”两个结果进行统计；并对植株吸收制剂的量(单位：mg)进行统计.规定：植株吸收在6mg（包括6mg）以上为“足量”，否则为“不足量”.现对该20株植株样本进行统计，其中 “植株存活”的13株，对制剂吸收量统计得下表.已知“植株存活”但“制剂吸收不足量”的植株共1株.

    编号

    01

    02

    03

    04

    05

    06

    07

    08

    09

    10

    11

    12

    13

    14

    15

    16

    17

    18

    19

    20

    吸收量(mg)

    6

    8

    3

    8

    9

    5

    6

    6

    2

    7

    7

    5

    10

    6

    7

    8

    8

    4

    6

    9

    （1）完成以下列联表，并判断是否可以在犯错误概率不超过1%的前提下，认为“植株的存活”与“制剂吸收足量”有关？

    吸收足量

    吸收不足量

    合计

    植株存活

    1

    植株死亡

    合计

    20

    （2）①若在该样本“吸收不足量”的植株中随机抽取3株，记为“植株死亡”的数量，求得分布列和期望；

    ②将频率视为概率，现在对已知某块种植了1000株并感染了病毒的该植物试验田里进行该药品喷雾试验，设“植株存活”且“吸收足量”的数量为随机变量，求.

    参考数据：，其中

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C：（）的两焦点与短轴的一个端点的连线构成等腰直角三角形，直线与以椭圆C的右焦点为圆心，以椭圆的半长轴长为半径的圆相切．

    （1）求椭圆C的方程；

    （2）设P为椭圆C上一点，若过点的直线l与椭圆C相交于不同的两点S和T，满足（O为坐标原点），求实数t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法：

    ①对于独立性检验，的值越大，说明两事件相关程度越大；

    ②以模型去拟合一组数据时，为了求出回归方程，设，将其变换后得到线性方程，则，的值分别是和0.3；

    ③已知随机变量，若，则（）的值为；

    ④通过回归直线及回归系数，可以精确反映变量的取值和变化趋势．

    其中错误的选项是（ ）

    A.①B.②C.③D.④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“过大年，吃水饺”是我国不少地方过春节的一大习俗，2020年春节前夕，A市某质检部门随机抽取了100包某种品牌的速冻水饺，检测其某项质量指标．

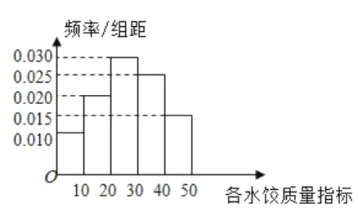
    （1）求所抽取的100包速冻水饺该项质量指标值的样本平均数（同一组中的数据用该组区间的中点值作代表）；

    （2）①由直方图可以认为，速冻水饺的该项质量指标值服从正态分布，利用该正态分布，求落在内的概率；

    ②将频率视为概率，若某人从某超市购买了4包这种品牌的速冻水饺，记这4包速冻水饺中这种质量指标值位于内的包数为，求的分布列和数学期望．

    附：①计算得所抽查的这100包速冻水饺的质量指标的标准差为；

    ②若，则，．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】关于函数有下述四个结论：

    ①函数的图象把圆的面积两等分

    ②是周期为的函数

    ③函数在区间上有个零点

    ④函数在区间上单调递减

    其中所有不正确结论的编号是（ ）

    A.①③④B.②③C.①④D.①③

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若函数在时取得极值，求实数的值；

    （2）若对任意恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合A＝{x|y＝ln（﹣x2﹣x+12）}，B＝{x|m﹣1＜x＜2m+1，m∈R}．

    （1）若m＝2，求（RA）∩B；

    （2）若A∩B＝B，求实数m的取值范围．

    查看答案和解析>>

    同步练习册答案