
设函数f(x)=(x2+ax+b)ex(x∈R).
(1)若a=2,b=-2,求函数f(x)的极大值;
(2)若x=1是函数f(x)的一个极值点.
①试用a表示b;
②设a>0,函数g(x)=(a2+14)ex+4.若?ξ1、ξ2∈[0,4],使得|f(ξ1)-g(ξ2)|<1成立,求a的取值范围.
(1)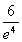 (2)①b=-3-2a②1-
(2)①b=-3-2a②1- <a<1+
<a<1+ .
.
【解析】(1)∵f′(x)=(2x+a)ex+(x2+ax+b)ex=[x2+(2+a)x+(a+b)]ex,
当a=2,b=-2时,f(x)=(x2+2x-2)ex,
则f′(x)=(x2+4x)ex,
令f′(x)=0得(x2+4x)ex=0,
∵ex≠0,∴x2+4x=0,解得x=-4或x=0,
列表如下:
x | (-∞,-4) | -4 | (-4,0) | 0 | (0,+∞) |
f′(x) | + | 0 | - | 0 | + |
f(x) | ? | 极大值 | ? | 极小值 | ? |
∴当x=-4时,函数f(x)取极大值,f(x)极大值=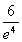 .
.
(2)①由(1)知f′(x)=[x2+(2+a)x+(a+b)]ex.
∵x=1是函数f(x)的一个极值点,∴f′(1)=0,
即e[1+(2+a)+(a+b)]=0,解得b=-3-2a.
②由①知f′(x)=ex[x2+(2+a)x+(-3-a)]=ex(x-1)[x+(3+a)],
当a>0时,f(x)在区间(0,1)上的单调递减,在区间(1,4)上单调递增,
∴函数f(x)在区间[0,4]上的最小值为f(1)=-(a+2)e.
∵f(0)=b=-3-2a<0,f(4)=(2a+13)e4>0,
∴函数f(x)在区间[0,4]上的值域是[f(1),f(4)],
即[-(a+2)e,(2a+13)e4].
又g(x)=(a2+14)ex+4在区间[0,4]上是增函数,且它在区间[0,4]上的值域是[(a2+14)e4,(a2+14)e8],
∴(a2+14)e4-(2a+13)e4=(a2-2a+1)e4=(a-1)2e4≥0,
∴存在ξ1、ξ2∈[0,4]使得|f(ξ1)-g(ξ2)|<1成立只须(a2+14)e4-(2a+13)e4<1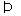 ?(a-1)2e4<1
?(a-1)2e4<1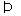 (a-1)2<
(a-1)2<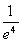 ?
?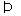 1-
1- <a<1+
<a<1+ .
.


科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第13课时练习卷(解析版) 题型:解答题
某公司为一家制冷设备厂设计生产某种型号的长方形薄板,其周长为4m.这种薄板须沿其对角线折叠后使用.如图所示,ABCD(AB>AD)为长方形薄板,沿AC折叠后AB′交DC于点P.当△ADP的面积最大时最节能,凹多边形ACB′PD的面积最大时制冷效果最好.
(1)设AB=xm,用x表示图中DP的长度,并写出x的取值范围;
(2)若要求最节能,应怎样设计薄板的长和宽?
(3)若要求制冷效果最好,应怎样设计薄板的长和宽?
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第12课时练习卷(解析版) 题型:解答题
已知函数f(x)=(ax2+x)ex,其中e是自然数的底数,a∈R.
(1)当a<0时,解不等式f(x)>0;
(2)若f(x)在[-1,1]上是单调函数,求a的取值范围;
(3)当a=0时,求整数k的所有值,使方程f(x)=x+2在[k,k+1]上有解.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第12课时练习卷(解析版) 题型:填空题
若存在正数x使2x(x-a)<1成立,则a的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第12课时练习卷(解析版) 题型:填空题
已知函数f(x)=- x2+blnx在区间[
x2+blnx在区间[ ,+∞)上是减函数,则b的取值范围是________.
,+∞)上是减函数,则b的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第11课时练习卷(解析版) 题型:填空题
已知函数f(x)=ex-f(0)x+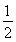 x2,则f′(1)=____.
x2,则f′(1)=____.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第10课时练习卷(解析版) 题型:填空题
若关于x的方程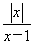 =kx2有四个不同的实数根,则实数k的取值范围是________.
=kx2有四个不同的实数根,则实数k的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第三章第8课时练习卷(解析版) 题型:解答题
如图,A、B是海面上位于东西方向相距5(3+ )海里的两个观测点,现位于A点北偏东45°、B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20
)海里的两个观测点,现位于A点北偏东45°、B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20 海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船达到D点需要多长时间?
海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船达到D点需要多长时间?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com