
如图,四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
(1)求证:PC⊥BC
(2)求点A到平面PBC的距离.
(1)BC⊥PC;(2) .
.
解析试题分析:(1)要证线线垂直,要从线面垂直角度入手,根据题中所给条件易知BC⊥平面PDC,而PC在平面PDC,从而能够证明出BC⊥PC. (2)要求点到面的距离,常用到等体积定理,由已知条件可知
VA-PBC=VP-ABC ,而通过计算可知VP-ABC=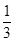 S△ABC·PD=
S△ABC·PD=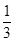 ,接下来只需要求出△PBC的面积,这样根据
,接下来只需要求出△PBC的面积,这样根据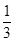 S△PBC·h=
S△PBC·h=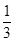 ,∴h=
,∴h= ,所以点A到平面PBC的距离为
,所以点A到平面PBC的距离为 .
.
试题解析:(1)∵PD⊥平面ABCD,BC?平面ABCD,∴PD⊥BC.
由∠BCD=90°知,BC⊥DC,
∵PD∩DC=D,∴BC⊥平面PDC,
∴BC⊥PC.
(2)设点A到平面PBC的距离为h,
∵AB∥DC,∠BCD=90°,∴∠ABC=90°,
∵AB=2,BC=1,∴S△ABC=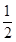 AB·BC=1,
AB·BC=1,
∵PD⊥平面ABCD,PD=1,
∴VP-ABC=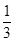 S△ABC·PD=
S△ABC·PD=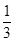 ,
,
∵PD⊥平面ABCD,∴PD⊥DC,
∵PD=DC=1,∴PC= ,
,
∵PC⊥BC,BC=1,
∴S△PBC=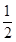 PC·BC=
PC·BC=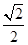 ,
,
∵VA-PBC=VP-ABC,
∴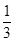 S△PBC·h=
S△PBC·h=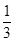 ,∴h=
,∴h= ,
,
∴点A到平面PBC的距离为 .
.
考点:1.线线垂直的证明;2.点到面的距离的求解.


科目:高中数学 来源: 题型:解答题
定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和两平面的交线平行.
请对上面定理加以证明,并说出定理的名称及作用.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知三棱柱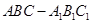 中,平面
中,平面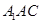 ⊥平面ABC,BC⊥AC,D为AC的中点,AC=BC=AA1=A1C=2。
⊥平面ABC,BC⊥AC,D为AC的中点,AC=BC=AA1=A1C=2。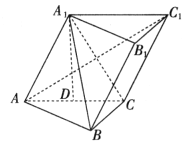
(Ⅰ)求证:AC1⊥平面A1BC;
(Ⅱ)求平面AA1B与平面A1BC的夹角的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.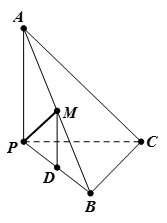
(1)求证:DM∥平面APC; (2)求证:平面ABC⊥平面APC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com