
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 先将函数进行参变量分离,得到2a=$\frac{{x}^{2}}{x+lnx}$,令g(x)=$\frac{{x}^{2}}{x+lnx}$,转化成y=2a与y=g(x)的图象的交点个数,利用导数得到函数的单调性,结合函数的图象可得结论.
解答 解:令f(x)=x2-2ax-2alnx=0,则2a(x+lnx)=x2,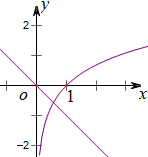
∴2a=$\frac{{x}^{2}}{x+lnx}$,令g(x)=$\frac{{x}^{2}}{x+lnx}$,
则g′(x)=$\frac{2x(x+lnx)-{x}^{2}(1+\frac{1}{x})}{({x+lnx)}^{2}}$=$\frac{x(x-1+2lnx)}{(x+lnx)^{2}}$
令h(x)=x+lnx,通过作出两个函数y=lnx及y=-x的图象(如右图)
发现h(x)有唯一零点在(0,1)上,
设这个零点为x0,当x∈(0,x0)时,g′(x)<0,g(x)在(0,x0)上单调递减,x=x0是渐近线,
当x∈(x0,1)时,g′(x)<0,则g(x)在(x0,1)上单调递减,
当x∈(1,+∞)时g′(x)>0,g(x)在(1,+∞)单调递增,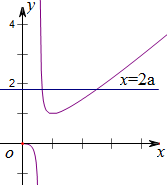
∴g(1)=1,可以作出g(x)=$\frac{{x}^{2}}{x+lnx}$的大致图象,
结合图象可知,当a<0时,y=2a与y=g(x)的图象只有一个交点,
则函数y=f(x)只有一个零点,故①正确;
若函数y=f(x)有零点,则a<0或a≥$\frac{1}{2}$,故②不正确;
存在a=$\frac{1}{2}$>0,函数y=f(x)有唯一零点,故③正确;
若函数y=f(x)有唯一零点,则a<0,或a=$\frac{1}{2}$,则a≤1,故④正确.
故选:B.
点评 本题考查了函数的零点与方程根的关系.函数的零点等价于对应方程的根,等价于函数的图象与x轴交点的横坐标,解题时要注意根据题意合理的选择转化.常运用数形结合的数学思想方法.属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 120° | B. | 60° | C. | 45° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2}{11}$ | B. | $\frac{2}{11}$ | C. | $\frac{11}{2}$ | D. | -$\frac{11}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
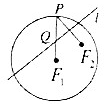 如图,已知圆F1的半径为4,|F1F2|=2,P是圆F1上的一个动点,F2P的中垂线l交F1P于点Q,以直线F1F2为x轴,F1F2的中垂线为y轴建立平面直角坐标系.
如图,已知圆F1的半径为4,|F1F2|=2,P是圆F1上的一个动点,F2P的中垂线l交F1P于点Q,以直线F1F2为x轴,F1F2的中垂线为y轴建立平面直角坐标系.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | 1-$\frac{π}{4}$ | C. | $\frac{{\sqrt{3}π}}{24}$ | D. | $1-\frac{{\sqrt{3}π}}{24}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” | |
| B. | “|x|<2”是“x2-x-6<0”的充分不必要条件 | |
| C. | 命题“存在∈R,使得x2+x+1<0”的否定是“对任意x∈R,均有x2+x+1≥0” | |
| D. | 若p∧q为假命题,则p,q均为假 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com