【答案】
分析:(I)将6,7,8分别进行分解,然后写出它们的一个分解积,使其值最大即可;
(II)由(Ⅰ)可知,a
k(k=1,2,…,n)中可以有2个2,当a
k(k=1,2,…,n)有3个或3个以上的2时,可举反例说明,从而证得结论;
(Ⅲ)讨论a
k(k=1,2,…,n)中有1,有2,有4的个数,以及有大于4的数,从而得到a
k(k=1,2,…,n)中只能出现2或3或4,且2不能超过2个,4不能超过1个,从而可得a
k(k=1,2,…,n),使得N的分解积最大.
解答:解:(Ⅰ)6=3+3,分解积的最大值为3×3=9; …(1分)
7=3+2+2=3+4,分解积的最大值为3×2×2=3×4=12; …(2分)
8=3+3+2,分解积的最大值为3×3×2=18. …(3分)
(Ⅱ)证明:由(Ⅰ)可知,a
k(k=1,2,…,n)中可以有2个2. …(4分)
当a
k(k=1,2,…,n)有3个或3个以上的2时,
因为2+2+2=3+3,且2×2×2<3×3,
所以,此时分解积不是最大的.
因此,
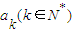
中至多有2个2. …(7分)
(Ⅲ)解:①当a
k(k=1,2,…,n)中有1时,
因为1+a
i=(a
i+1),且1×a
i<a
i+1,
所以,此时分解积不是最大,可以将1加到其他加数中,使得分解积变大.…(8分)
②由(Ⅱ)可知,a
k(k=1,2,…,n)中至多有2个2.
③当a
k(k=1,2,…,n)中有4时,
若将4分解为1+3,由 ①可知分解积不会最大;
若将4分解为2+2,则分解积相同;
若有两个4,因为4+4=3+3+2,且4×4<3×3×2,所以将4+4改写为3+3+2,使得分解积更大.
因此,a
k(k=1,2,…,n)中至多有1个4,而且可以写成2+2. …(10分)
④当a
k(k=1,2,…,n)中有大于4的数时,不妨设a
i>4,
因为a
i<2(a
i-2),
所以将a
i分解为2+(a
i-2)会使得分解积更大. …(11分)
综上所述,a
k(k=1,2,…,n)中只能出现2或3或4,且2不能超过2个,4不能超过1个.
于是,当N=3m(m∈N
*)时,
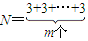
使得分解积最大; …(12分)
当N=3m+1(m∈N
*)时,

使得分解积最大; …(13分)
当N=3m+2(m∈N)时,
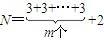
使得分解积最大.…(14分)
点评:本题主要考查了数列的综合应用,同时考查了分类讨论的数学思想,以及计算能力,属于难题.

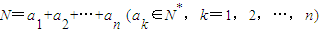 ,则称a1×a2×…×an为N的一个“分解积”.
,则称a1×a2×…×an为N的一个“分解积”.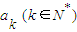 中2的个数不超过2;
中2的个数不超过2;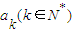 中至多有2个2. …(7分)
中至多有2个2. …(7分)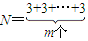 使得分解积最大; …(12分)
使得分解积最大; …(12分) 使得分解积最大; …(13分)
使得分解积最大; …(13分)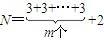 使得分解积最大.…(14分)
使得分解积最大.…(14分)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案