
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的一段图象如下所示.
)的一段图象如下所示. 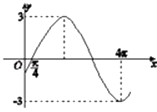
(1)求f(x)的解析式;
(2)求f(x)的单调减区间,并指出f(x)的最大值及取到最大值时x的集合.
【答案】
(1)解:由图象可以得到函数f(x)的振幅A=3,
设函数周期为T,则 ![]() ,
,
所以T=5π,则ω= ![]() ,
,
由ωx0+Φ=0,得 ![]() Φ=0,所以Φ=﹣
Φ=0,所以Φ=﹣ ![]() ,
,
所以f(x)=3sin ![]()
(2)解:由 ![]() ,
,
得 ![]() ,
,
所以函数的减区间为( ![]() +5kπ,4π+5kπ)k∈Z.
+5kπ,4π+5kπ)k∈Z.
函数f(x)的最大值为3,当且仅当 ![]() ,
,
即 ![]() 时函数取得最大值.
时函数取得最大值.
所以函数的最大值为3,取得最大值时的x的集合为{x|x= ![]() }
}
【解析】(1)由图象直接得到振幅A,和四分之三周期,所以周期可求,则ω可求,然后根据五点作图的第一点求得Φ,则函数解析式可求;(2)直接由三角函数符号后面的相位在正弦函数的减区间内求得函数的减区间,由终边在y轴正半轴上的角的正弦值最大求出使函数取得最大值时的角x的集合.
【考点精析】通过灵活运用正弦函数的单调性和三角函数的最值,掌握正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数;函数
上是减函数;函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() 即可以解答此题.
即可以解答此题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的左右焦点,
的左右焦点,![]() 为原点,
为原点,![]()
![]() 在椭圆上,线段
在椭圆上,线段![]() 与
与![]() 轴的交点
轴的交点![]() 满足
满足![]() .
.
(1)求椭圆的标准方程;
(2)过椭圆右焦点![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,若
点,若![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了展示中华汉字的无穷魅力,传递传统文化,提高学习热情,某校开展《中国汉字听写大会》的活动.为响应学校号召,2(9)班组建了兴趣班,根据甲、乙两人近期8次成绩画出茎叶图,如图所示,甲的成绩中有一个数的个位数字模糊,在茎叶图中用![]() 表示.(把频率当作概率).
表示.(把频率当作概率).

(1)假设![]() ,现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
,现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
(2)假设数字![]() 的取值是随机的,求乙的平均分高于甲的平均分的概率.
的取值是随机的,求乙的平均分高于甲的平均分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家拟在2017年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)![]() (单位:万件)与年促销费用
(单位:万件)与年促销费用![]() (单位:万元)(
(单位:万元)(![]() )满足
)满足![]() (
(![]() 为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2017年生产该产品的固定投入为8万元.每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2017年生产该产品的固定投入为8万元.每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2017年该产品的利润![]() (单位:万元)表示为年促销费用
(单位:万元)表示为年促销费用![]() (单位:万元)的函数;
(单位:万元)的函数;
(2)该厂家2017年的促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】运货卡车以每小时![]() 千米的速度匀速行驶
千米的速度匀速行驶![]() 千米(
千米(![]() ).假设汽油的价格是每升
).假设汽油的价格是每升![]() 元,而汽车每小时耗油
元,而汽车每小时耗油 升,司机的工资是每小时
升,司机的工资是每小时![]() 元.
元.
(1)求这次行车总费用![]() 关于
关于![]() 的表达式;
的表达式;
(2)当![]() 为何值时,这次行车的总费用最低?并求出最低费用的值.
为何值时,这次行车的总费用最低?并求出最低费用的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合![]() .如果对于
.如果对于![]() 的每一个含有
的每一个含有![]() 个元素的子集
个元素的子集![]() ,
, ![]() 中必有4个元素的和等于
中必有4个元素的和等于![]() ,称正整数
,称正整数![]() 为集合
为集合![]() 的一个“相关数”.
的一个“相关数”.
(Ⅰ)当![]() 时,判断5和6是否为集合
时,判断5和6是否为集合![]() 的“相关数”,说明理由;
的“相关数”,说明理由;
(Ⅱ)若![]() 为集合
为集合![]() 的“相关数”,证明:
的“相关数”,证明: ![]() ;
;
(Ⅲ)给定正整数![]() .求集合
.求集合![]() 的“相关数”
的“相关数” ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的前n项和Sn , 首项a1=a,公比为q(q≠0且q≠1).
(1)推导证明:Sn= ![]() ;
;
(2)等比数列{an}中,是否存在连续的三项:ak、ak+1、ak+2 , 使得这三项成等差数列?若存在,求出符合条件的等比数列公比q的值,若不存在,说明理由;
(3)本题中,若a=q=2,已知数列{nan}的前n项和Tn , 是否存在正整数n,使得Tn≥2016?若存在,求出n的取值集合;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com