
分析 (1)根据方程x2+y2+Dx+Ey+F=0表示圆的条件,结合题意求出F的取值范围;
(2)根据题意求出r和d,计算d2-r2的值即可;
(3)存在定圆M:x2+y2=1满足题意,证明圆M与直线l相切,并且圆M与圆C相离即可.
解答 解:(1)方程x2+y2+Dx+Ey+F=0表示圆,
则D2+E2>4F,
又D2+E2=F2,且F>0,
所以中F2>4F,且F>0,
解得F>4; …(3分)
(2)圆C:x2+y2+Dx+Ey+F=0的圆心为C(-$\frac{D}{2}$,-$\frac{E}{2}$),
半径r=$\frac{\sqrt{{D}^{2}{+E}^{2}-4F}}{2}$=$\frac{\sqrt{{F}^{2}-4F}}{2}$,
圆心C到直线l的距离为
d=$\frac{|D×(-\frac{D}{2})+E×(-\frac{E}{2})+F|}{\sqrt{{D}^{2}{+E}^{2}}}$=|$\frac{F-2}{2}$|,
所以d2-r2=${|\frac{F-2}{2}|}^{2}$-${(\frac{\sqrt{{F}^{2}-4F}}{2})}^{2}$=1; …(8分)
(3)存在定圆M:x2+y2=1满足题意,下证之:…(10分)
1°因为M(0,0)到直线l的距离为$\frac{|F|}{\sqrt{{D}^{2}{+E}^{2}}}$=1=R,
所以圆M与直线l相切;
2°因为CM=$\sqrt{{(0+\frac{D}{2})}^{2}{+(0+\frac{E}{2})}^{2}}$=$\frac{F}{2}$,且R+1=$\frac{\sqrt{{F}^{2}-4F}}{2}$+1,
而$\frac{F}{2}$>$\frac{\sqrt{{F}^{2}-4F}}{2}$+1,
即${(\frac{F}{2}-1)}^{2}$>$\frac{{F}^{2}-4F}{4}$,
即4>0,
故CM>R+1,
所以圆M与圆C相离;
由1°、2°得,存在定圆M:x2+y2=1满足题意. …(16分)
点评 本题考查了直线与圆的方程与应用问题,也考查了点到直线的距离问题的应用,是综合性问题.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
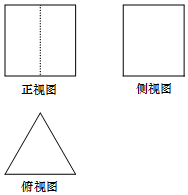 某几何体的三视图如图所示,其中正视图是边长为2的正方形,俯视图是正三角形,则这个几何体的体积是( )
某几何体的三视图如图所示,其中正视图是边长为2的正方形,俯视图是正三角形,则这个几何体的体积是( )| A. | $2\sqrt{3}$ | B. | $4\sqrt{3}$ | C. | $\frac{2}{3}\sqrt{3}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
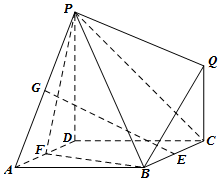 如图所示的多面体中,面ABCD是边长为2的正方形,平面PDCQ⊥平面ABCD,PD⊥DC,E,F,G分别为棱BC,AD,PA的中点.
如图所示的多面体中,面ABCD是边长为2的正方形,平面PDCQ⊥平面ABCD,PD⊥DC,E,F,G分别为棱BC,AD,PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
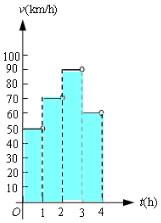 一辆汽车在某段路程中的行驶速率与时间的关系如图所示.
一辆汽车在某段路程中的行驶速率与时间的关系如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,直线l是曲线y=f(x)在x=3处的切线,f'(x)表示函数f(x)的导函数,则f(3)+f'(3)的值为$\frac{7}{3}$.
如图,直线l是曲线y=f(x)在x=3处的切线,f'(x)表示函数f(x)的导函数,则f(3)+f'(3)的值为$\frac{7}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com