
°æƒø°øƒ≥π§≥ߌ™¡À∂‘–¬—–∑¢µƒ“ª÷÷≤˙∆∑Ω¯––∫œ¿Ì∂®º€£¨Ω´∏√≤˙∆∑∞¥ ¬œ»ƒ‚∂®µƒº€∏ÒΩ¯–– ‘œ˙£¨µ√µΩ»Áœ¬ ˝æð£∫
µ•º€x£®‘™£© | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
œ˙¡øy£®º˛£© | 90 | 84 | 83 | 80 | 75 | 68 |
£®1£©«ÛªÿπÈ÷±œþ∑Ω≥à ![]() =
= ![]() x+
x+ ![]() £¨∆‰÷–
£¨∆‰÷– ![]() =©Å20£¨
=©Å20£¨ ![]() =
= ![]() ©Å
©Å ![]()
![]()
£®2£©‘§º∆‘⁄ΩÒ∫Ûµƒœ˙ €÷–£¨œ˙¡ø”ε•º€»‘»ª∑˛¥”£®1£©÷–µƒπÿœµ£¨«“∏√≤˙∆∑µƒ≥…±æ «4‘™/º˛£¨Œ™ ππ§≥ߪҵ√◊Ó¥Û¿˚»Û£¨∏√≤˙∆∑µƒµ•º€”¶∂®Œ™∂ý…Ÿ‘™£ø£®¿˚»Û=œ˙ € ’»Î©Å≥…±æ£©
°æ¥∞∏°ø
£®1£©Ω‚£∫ ![]() =
= ![]() £®8+8.2+8.4+8.6+8.8+9£©=8.5£¨
£®8+8.2+8.4+8.6+8.8+9£©=8.5£¨
![]() =
= ![]() £®90+84+83+80+75+68£©=80£ª
£®90+84+83+80+75+68£©=80£ª
°þy= ![]() x+
x+ ![]() £¨
£¨ ![]() =©Å20
=©Å20
°ý80=©Å20°¡8.5+ ![]() £¨
£¨
°ý ![]() =250
=250
°ý ![]() =©Å20x+250£Æ
=©Å20x+250£Æ
£®2£©Ω‚£∫…Ëπ§≥ߪҵ√µƒ¿˚»ÛŒ™L‘™£¨‘Ú
L=x£®©Å20x+250£©©Å4£®©Å20x+250£©=©Å20 ![]() +361.25£¨
+361.25£¨
°ý∏√≤˙∆∑µƒµ•º€”¶∂®Œ™ ![]() ‘™ ±£¨π§≥ߪҵ√µƒ¿˚»Û◊Ó¥Û£Æ
‘™ ±£¨π§≥ߪҵ√µƒ¿˚»Û◊Ó¥Û£Æ
°æΩ‚Œˆ°ø£®1£©¿˚”√ªÿπÈ÷±œþπ˝—˘±æµƒ÷––ƒµ„£® ![]() £¨
£¨ ![]() £©£¨º¥ø…«Û≥ˆªÿπÈ÷±œþ∑Ω≥㪣®2£©…Ëπ§≥ߪҵ√¿˚»ÛŒ™L‘™£¨¿˚”√¿˚»Û=œ˙ € ’»Î©Å≥…±æ£¨Ω®¡¢∫Ø ˝πÿœµ£¨”√≈‰∑Ω∑®«Û≥ˆπ§≥ߪҵ√µƒ◊Ó¥Û¿˚»Û£Æ
£©£¨º¥ø…«Û≥ˆªÿπÈ÷±œþ∑Ω≥㪣®2£©…Ëπ§≥ߪҵ√¿˚»ÛŒ™L‘™£¨¿˚”√¿˚»Û=œ˙ € ’»Î©Å≥…±æ£¨Ω®¡¢∫Ø ˝πÿœµ£¨”√≈‰∑Ω∑®«Û≥ˆπ§≥ߪҵ√µƒ◊Ó¥Û¿˚»Û£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄R…œ∂®“‘ÀÀ„°—£∫a°—b=ab+2a+b£¨‘Ú¬˙◊„x°—£®x©Å2£©£º0µƒ µ ˝xµƒ»°÷µ∑∂ŒßŒ™ £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™’˝œÓ ˝¡–{an}µƒ«∞nœÓ∫ÕŒ™Sn £¨ «“2Sn=£®an©Å1£©£®an+2£©£¨
£®1£©«Û ˝¡–{an}µƒÕ®œÓπ´ Ω
£®2£©…Ë ˝¡–{ ![]() }µƒ«∞nœÓ∫ÕŒ™Tn £¨ ‘±»ΩœTn”Î
}µƒ«∞nœÓ∫ÕŒ™Tn £¨ ‘±»ΩœTn”Î ![]() µƒ¥Û–°£Æ
µƒ¥Û–°£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øΩ´∫Ø ˝y=sinxµƒÕºœÛæ≠π˝œ¬¡–ƒƒ÷÷±‰ªªø…“‘µ√µΩ∫Ø ˝y=cos2xµƒÕºœÛ£® £©
A.œ»œÚ◊Û∆Ω“∆ ![]() ∏ˆµ•Œª£¨»ª∫Û‘Ÿ—ÿx÷·Ω´∫·◊¯±Í—πÀıµΩ‘≠¿¥µƒ
∏ˆµ•Œª£¨»ª∫Û‘Ÿ—ÿx÷·Ω´∫·◊¯±Í—πÀıµΩ‘≠¿¥µƒ ![]() ±∂£®◊ð◊¯±Í≤ª±‰£©
±∂£®◊ð◊¯±Í≤ª±‰£©
B.œ»œÚ◊Û∆Ω“∆ ![]() ∏ˆµ•Œª£¨»ª∫Û‘Ÿ—ÿx÷·Ω´∫·◊¯±Í…Ï≥§µΩ‘≠¿¥µƒ2±∂£®◊ð◊¯±Í≤ª±‰£©
∏ˆµ•Œª£¨»ª∫Û‘Ÿ—ÿx÷·Ω´∫·◊¯±Í…Ï≥§µΩ‘≠¿¥µƒ2±∂£®◊ð◊¯±Í≤ª±‰£©
C.œ»œÚ◊Û∆Ω“∆ ![]() ∏ˆµ•Œª£¨»ª∫Û‘Ÿ—ÿx÷·Ω´∫·◊¯±Í—πÀıµΩ‘≠¿¥µƒ
∏ˆµ•Œª£¨»ª∫Û‘Ÿ—ÿx÷·Ω´∫·◊¯±Í—πÀıµΩ‘≠¿¥µƒ ![]() ±∂£®◊ð◊¯±Í≤ª±‰£©
±∂£®◊ð◊¯±Í≤ª±‰£©
D.œ»œÚ◊Û∆Ω“∆ ![]() ∏ˆµ•Œª£¨»ª∫Û‘Ÿ—ÿx÷·Ω´∫·◊¯±Í…Ï≥§µΩ‘≠¿¥µƒ2±∂£®◊ð◊¯±Í≤ª±‰£©
∏ˆµ•Œª£¨»ª∫Û‘Ÿ—ÿx÷·Ω´∫·◊¯±Í…Ï≥§µΩ‘≠¿¥µƒ2±∂£®◊ð◊¯±Í≤ª±‰£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝f£®x£©=Asin£®¶ÿx+¶’£©£®¶ÿ£æ0£¨0£º¶’£º ![]() £©µƒ≤ø∑÷ÕºœÛ»ÁÕº£Æ
£©µƒ≤ø∑÷ÕºœÛ»ÁÕº£Æ 
£®1£©«Ûf£®x£©µƒΩ‚Œˆ Ω£ª
£®2£©Ω´∫Ø ˝y=f£®x£©µƒÕºœÛ…œÀ˘”–µ„µƒ◊ð◊¯±Í≤ª±‰£¨∫·◊¯±ÍÀı∂ÃŒ™‘≠¿¥µƒ ![]() ±∂£¨‘ŸΩ´À˘µ√∫Ø ˝ÕºœÛœÚ”“∆Ω“∆
±∂£¨‘ŸΩ´À˘µ√∫Ø ˝ÕºœÛœÚ”“∆Ω“∆ ![]() ∏ˆµ•Œª£¨µ√µΩ∫Ø ˝y=g£®x£©µƒÕºœÛ£¨«Ûg£®x£©µƒµ•µ˜µð‘ˆ«¯º‰£Æ
∏ˆµ•Œª£¨µ√µΩ∫Ø ˝y=g£®x£©µƒÕºœÛ£¨«Ûg£®x£©µƒµ•µ˜µð‘ˆ«¯º‰£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄Àƒ¿‚◊∂![]() ÷–£¨µ◊√Ê
÷–£¨µ◊√Ê![]() «Ã𖌣¨
«Ã𖌣¨ ![]() £¨
£¨ ![]() £¨
£¨ ![]() £¨
£¨ ![]() £¨≤ý√Ê
£¨≤ý√Ê![]() µ◊√Ê
µ◊√Ê![]() .
.
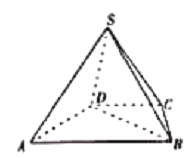
£®1£©«Û÷§£∫∆Ω√Ê![]() ∆Ω√Ê
∆Ω√Ê![]() £ª
£ª
£®2£©»Ù![]() ”ε◊√Ê
”ε◊√Ê![]() À˘≥…Ω«Œ™
À˘≥…Ω«Œ™![]() £¨«Û∂˛√ÊΩ«
£¨«Û∂˛√ÊΩ«![]() µƒ”ýœ“÷µ.
µƒ”ýœ“÷µ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄π´≤Ó≤ªŒ™¡„µƒµ»≤Ó ˝¡–{an}∫Õµ»±» ˝¡–{bn}÷–£Æ“—÷™a1=b1=1£Æa2=b2 £Æ a6=b3
£®1£©«Ûµ»≤Ó ˝¡–{an}µƒÕ®œÓπ´ Ωan∫Õµ»±» ˝¡–{bn}µƒÕ®œÓπ´ Ωbn£ª
£®2£©«Û ˝¡–{anbn}µƒ«∞nœÓ∫ÕSn £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™≤ªµ» Ω◊È 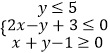 ±Ì 浃∆Ω√Ê«¯”ÚŒ™D£¨»Ù£®x£¨y£©° D£¨|x|+2y°ÐaŒ™’Ê√¸Ã‚£¨‘Ú µ ˝aµƒ»°÷µ∑∂Œß «£® £©
±Ì 浃∆Ω√Ê«¯”ÚŒ™D£¨»Ù£®x£¨y£©° D£¨|x|+2y°ÐaŒ™’Ê√¸Ã‚£¨‘Ú µ ˝aµƒ»°÷µ∑∂Œß «£® £©
A.[10£¨+°Þ£©
B.[11£¨+°Þ£©
C.[13£¨+°Þ£©
D.[14£¨+°Þ£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com