练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在四棱锥中，底面为直角梯形，，，平面底面，为的中点，是棱上的点，，，．

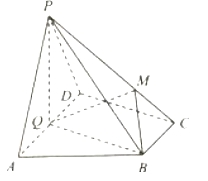
    （1）求证：平面平面；

    （2）若，求二面角的大小．

    【答案】（1）证明见解析；（2）．

    【解析】

    试题分析：（1）借助题设条件运用面面垂直的判定定理推证；（2）借助题设运用空间向量的数量积公式求解．

    试题解析：

    （1）∵为的中点，，，

    ∴，，∴四边形是平行四边形，∴，

    ∵底面为直角梯形，，，∴．

    又，∴平面．∵平面，∴平面平面．…………6分

    （2）∵，平面底面，平面底面，

    ∴底面，

    以为原点，为轴，为轴，为轴，建立空间直角坐标系，

    则，，，，

    设，则，

    即，

    ∴，，，∴，

    ，，

    设平面的法向量，则，

    取，得，平面的法向量．

    设二面角的平面角为，则，

    ∴，

    ∴二面角的大小为．………………12分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知数列中，，点（）在直线y = x上，

    （Ⅰ）计算a2，a3，a4的值；

    （Ⅱ）令bn=an+1﹣an﹣1，求证：数列{bn}是等比数列；

    （Ⅲ）设Sn、Tn分别为数列{an}、{bn}的前n项和，是否存在实数λ，使得数列为等差数列？若存在，试求出λ的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的一个焦点与短轴的两个端点是正三角形的三个项点，点在椭圆上．

    （1）求椭圆的方程；

    （2）设不过原点且斜率为的直线与椭圆交于不同的两点，线段的中点为，直线与椭圆交于，证明：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，某生态园将一三角形地块的一角开辟为水果园种植桃树，已知角为,的长度均大于米，现在边界处建围墙，在处围竹篱笆．

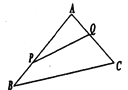
    （1）若围墙总 长度为米，如何围可使得三角形地块的面积最大？

    （2）已知段围墙高米，段围墙高米，造价均为每平方米元．若围围墙用了元,问如何围可使竹篱笆用料最省？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）求函数在点处的切线方程；

    （2）求函数单调递增区间；

    （3）若存在，使得（是自然对数的底数），求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设椭圆的左右焦点分别为，，点满足．

    (Ⅰ) 求椭圆的离心率；

    (Ⅱ) 设直线与椭圆相交于两点，若直线与圆相交于，两点，且，求椭圆的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】 在一个特定时段内，以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东且与点A相距40海里的位置B，经过40分钟又测得该船已行驶到点A北偏东+(其中sin=，)且与点A相距10海里的位置C.

    （I）求该船的行驶速度（单位：海里/小时）;

    （II）若该船不改变航行方向继续行驶.判断它是否会进入警戒水域，并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线被圆所截得的弦长为8.

    （1）求圆的方程；

    （2）若直线与圆切于点，当直线与轴正半轴，轴正半轴围成的三角形面积最小时，求点的坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下列结论：

    动点分别到两定点（-3,0）、（3,0） 连线的斜率之乘积为，设的轨迹为曲线，分别为曲线的左、右焦点，则下列说法中：

    （1）曲线的焦点坐标为；

    （2）当时，的内切圆圆心在直线上；

    （3）若，则；

    （4）设，则的最小值为；

    其中正确的序号是：_____________．

    查看答案和解析>>

    同步练习册答案