
分析 (1)根据题意,由函数的解析式可得f(0)的值,即可得f(0)+4的值,进而代入函数解析式计算可得f[f(0)+4]的值;
(2)由作差法证明:设x1,x2∈R且x1<x2,化简并分析f(x1)-f(x2)的符号,即可得证明.
解答 解:(1)根据题意,函数f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$,
则f(0)=$\frac{{2}^{0}-1}{{2}^{0}+1}$=0,∴f[f(0)+4]=f(4)=$\frac{{2}^{4}-1}{{2}^{4}+1}$=$\frac{15}{17}$.
(2)证明 设x1,x2∈R且x1<x2,则${2^{x_2}}$>${2^{x_1}}$>0,${2^{x_2}}$-${2^{x_1}}$>0,
f(x1)-f(x2)=($\frac{{2}^{{x}_{1}}-1}{{2}^{{x}_{1}}+1}$)-($\frac{{2}^{{x}_{2}}-1}{{2}^{{x}_{2}}+1}$)=-$\frac{2({2}^{{x}_{2}}-{2}^{{x}_{1}})}{({2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)}$<0,
即f(x1)<f(x2),所以f(x)在R上是增函数.
点评 本题考查函数单调性的判定、证明,关键是掌握定义法证明函数单调性的方法.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
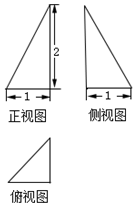
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数 | B. | 减函数 | ||
| C. | 既是奇函数又是减函数 | D. | 不是奇函数也不是减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 价格x/元 | 14 | 16 | 18 | 20 | 22 |
| 需求量y/件 | 56 | 50 | 3 | 1 | 37 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com