
【题目】如图,三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 分别为棱
分别为棱![]() 的中点.
的中点.
(1)在平面![]() 内过点
内过点![]() 作
作![]() 平面
平面![]() 交
交![]() 于点
于点![]() ,并写出作图步骤,但不要求证明.
,并写出作图步骤,但不要求证明.
(2)若侧面![]() 侧面
侧面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
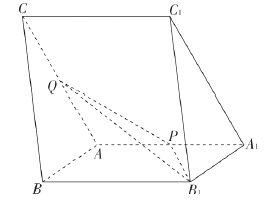
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)证线面平行则需在面内找一线与之平行即可平面![]() 内,过点
内,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() ,在
,在![]() 中,作
中,作![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() 并延长交
并延长交![]() 于点
于点![]() ,则
,则![]() 为所求作直线.(2)根据图形分别以
为所求作直线.(2)根据图形分别以![]() 的方向为
的方向为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴的正方向,然后写出
轴的正方向,然后写出![]() 的坐标,求出面
的坐标,求出面![]() 得法向量m,根据
得法向量m,根据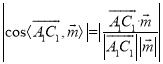 即可求得结果.
即可求得结果.
试题解析:
(1)如图,在平面![]() 内,过点
内,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() ,在
,在![]() 中,作
中,作![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() 并延长交
并延长交![]() 于点
于点![]() ,则
,则![]() 为所求作直线.
为所求作直线.
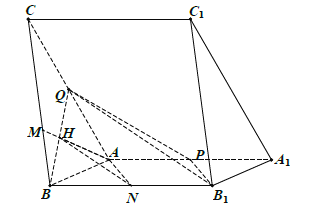
(2)连结![]() ,∵
,∵![]() ,∴
,∴![]() 为正三角形.
为正三角形.
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() ,
,
又∵侧面![]() 侧面
侧面![]() ,且面
,且面![]() 面
面![]() ,
,
![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
在平面![]() 内过点
内过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,
分别以![]() 的方向为
的方向为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴的正方向,建立如图所示的空间直角坐标系
轴的正方向,建立如图所示的空间直角坐标系![]() ,则
,则![]() ,
, ![]() .
.
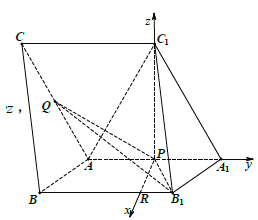
∵![]() 为
为![]() 的中点,∴点
的中点,∴点![]() 的坐标为
的坐标为![]() ,
,
∴![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
由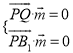 得
得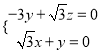 ,
,
令![]() ,得
,得![]() ,所以平面
,所以平面![]() 的一个法向量为
的一个法向量为![]() .
.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则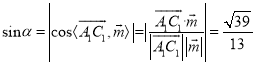 ,
,
即直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=mx2﹣mx﹣1.
(1)若对于x∈R,f(x)<0恒成立,求实数m的取值范围;
(2)若对于x∈[1,3],f(x)<5﹣m恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 为参数),
为参数),![]() 为参数).
为参数).
(1)化![]() 的参数方程为普通方程,并说明它们分别表示什么曲线;
的参数方程为普通方程,并说明它们分别表示什么曲线;
(2)若![]() 上的点
上的点![]() 对应的参数为
对应的参数为![]() 为
为![]() 上的动点,求
上的动点,求![]() 的中点
的中点![]() 到直线
到直线![]() 为参数)距离的最小值.
为参数)距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn= ![]() ,n∈N* .
,n∈N* .
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn= ![]() +(﹣1)nan , 求数列{bn}的前2n项和.
+(﹣1)nan , 求数列{bn}的前2n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校大一新生中的6名同学打算参加学校组织的“演讲团”、“吉他协会”等五个社团,若每名同学必须参加且只能参加1个社团且每个社团至多两人参加,则这6个人中没有人参加“演讲团”的不同参加方法数为( )
A. 3600 B. 1080 C. 1440 D. 2520
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场拟对某商品进行促销,现有两种方案供选择,每种促销方案都需分两个月实施,且每种方案中第一个月与第二个月的销售相互独立.根据以往促销的统计数据,若实施方案1,预计第一个月的销量是促销前的1.2倍和1.5倍的概率分别是0.6和0.4,第二个月的销量是第一个月的1.4倍和1.6倍的概率都是0.5;若实施方案2,预计第一个月的销量是促销前的1.4倍和1.5倍的概率分别是0.7和0.3,第二个月的销量是第一个月的1.2倍和1.6倍的概率分别是0.6和0.4.令![]() 表示实施方案
表示实施方案![]() 的第二个月的销量是促销前销量的倍数.
的第二个月的销量是促销前销量的倍数.
(Ⅰ)求![]() ,
, ![]() 的分布列;
的分布列;
(Ⅱ)不管实施哪种方案, ![]() 与第二个月的利润之间的关系如下表,试比较哪种方案第二个月的利润更大.
与第二个月的利润之间的关系如下表,试比较哪种方案第二个月的利润更大.
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)过点A(2,0),B(0,1)两点.
=1(a>b>0)过点A(2,0),B(0,1)两点.
(1)求椭圆C的方程及离心率;
(2)设直线l与椭圆相交于不同的两点A,B.已知点A的坐标为(﹣a,0),点 Q(0,y0)在线段AB的垂直平分线上,且 ![]()
![]() =4,求y0的值.
=4,求y0的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的几何体中,四边形AA1B1B是边长为3的正方形,CC1=2,CC1∥AA1 , 这个几何体是棱柱吗?若是,指出是几棱柱.若不是棱柱,请你试用一个平面截去一部分,使剩余部分是一个棱长为2的三棱柱,并指出截去的几何体的特征,在立体图中画出截面. 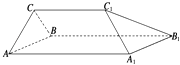
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图⑴、⑵、⑶、⑷为四个几何体的三视图,根据三视图可以判断这四个几何体依次分别为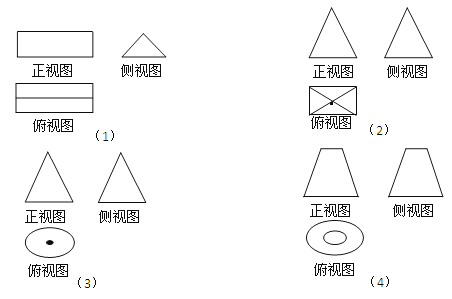
A.三棱台、三棱柱、圆锥、圆台
B.三棱台、三棱锥、圆锥、圆台
C.三棱柱、正四棱锥、圆锥、圆台
D.三棱柱、三棱台、圆锥、圆台
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com